Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 2

Тобто кожен із них набуває значення 1 тільки при , а для решти заданих значень аргумента він дорівнює нулю. Такі поліноми одержали назву  лагранжевих коефіцієнтів, або множників впливу відповідних вузлів інтерполювання.

  Щоб виконувалася перша умова (5.2), поліном  повинен мати такий вигляд

, (5.3)

тобто добутку  різниць між поточним значенням аргумента й одним із заданих, окрім -го, з деяким коефіцієнтом . Друга умова (5.2) дозволяє визначити цей коефіцієнт . Для цього в (5.3) слід покласти  і прирівняти результат до одиниці. З цього матимемо

.

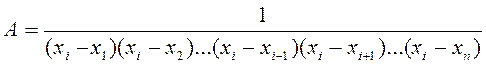  Враховуючи це, одержимо остаточний вигляд допоміжного полінома

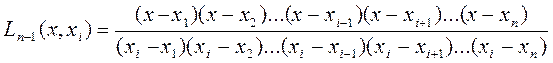.(5.4)

Тепер шуканий інтерполюючий поліном можна подати у вигляді

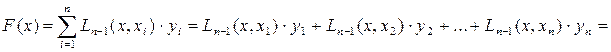
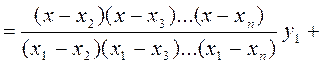
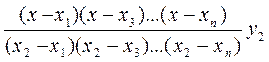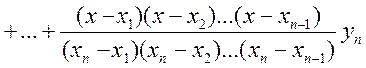+.                                (5.5)

Це і є інтерполяційний поліном Лагранжа степеня . Кількість арифметичних операцій для його обчислення дорівнює . Інтерполювання за Лагранжем зручно використовувати тоді, коли ведеться багаторазове інтерполювання різних функцій за однакових значень масиву аргументів. Тоді можна заздалегідь одноразово обчислити коефіцієнти Лагранжа, оскільки вони не залежать від функції, що інтерполюється.

  Розглянемо  деякі часткові випадки.

1 Лінійна інтерполяція

У цьому разі маємо  два вузли інтерполяції. Інтерполяційний поліном Лагранжа має  вигляд:

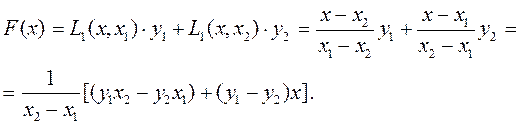(5.6)

2 Квадратична інтерполяція

У цьому випадку є три вузли інтерполяції (). Інтерполяційний поліном Лагранжа набирає вигляду:

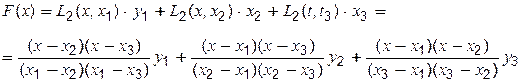(5.7)

5.2.2. Інтерполювання за Ньютоном

  Недоліком інтерполювання за Лагранжем є те, що якщо для поліпшення наближення додати ще один вузол інтерполювання, доведеться всі обчислення проводити заново.

  На практиці часто трапляються випадки, коли вузли інтерполяції стають відомими не одразу, а поступово, один за одним,  наприклад, у процесі вимірювання. Тоді зручно побудувати процес інтерполювання у такий спосіб, щоб поява даних про новий вузол інтерполювання, призводила б до необхідності мінімального перерахунку попередніх обчислень. Саме таку властивість має інтерполювання за Ньютоном.

  Нехай вузли інтерполяції рівновіддалені один від одного за аргументом, тобто виконується умова

;                 ().   (5.8)

Різниці

                          (5.9)

називають скінченними різницями першого порядку. Різниці сусідніх скінченних різниць першого порядку

          (5.10)

називають скінченними різницями другого порядку. Аналогічно

                       (5.11)

є скінченними різницями -го порядку. Вони визначаються за формулою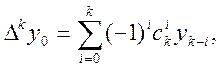  де -біноміальні коефіцієнти.

Розглянемо поліном

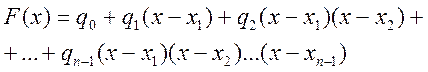.  (5.12)

Визначимо його коефіцієнти. Коефіцієнт  визначимо з умови проходження полінома через першу точку  ()

.                                  (5.13)

З умови проходження полінома через точку () одержимо значення 

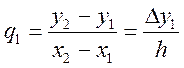;.       (5.14)

Аналогічно визначається решта коефіцієнтів

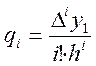.                                (5.15)

Підставляючи отримані вирази у (5.12), одержуємо

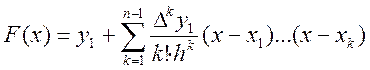.          (5.16)

Це є перша інтерполяційна формула Ньютона (формула інтерполювання вперед).

Як бачимо, особливостями інтерполювання за Ньютоном є:

n при появі нового вузла додається лише новий член, решта не перераховується;

n коефіцієнти швидко зменшуються зі зростанням , бо у знаменнику міститься факторіал від .

  Іноді використовується формула для інтерполювання назад

.

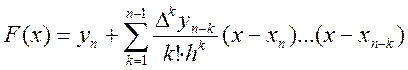Візьмемо деяку функцію  f(x)R і систему вузлів інтерполяції ,  ,  при іj. Вузли інтерполяції не є рівновіддаленими. Для цієї функції і вузлів утворимо  відношення

    .

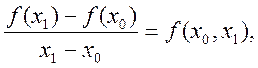
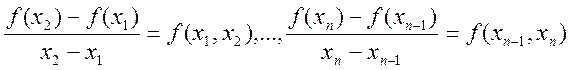  Вони називаються розділеними різницями першого порядку. Одержавши їх, ми можемо утворити нові відношення

…,

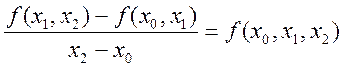
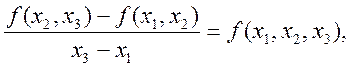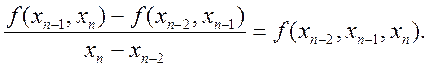
Вони називаються розділеними різницями другого порядку. Взагалі, якщо ми уже визначили розділені різниці k-го порядку ,то розділені різниці (k+1)-го порядку знаходяться за допомогою формули

 .

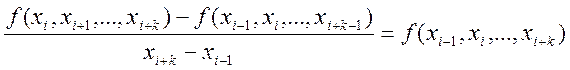Іноді замість  для позначення розділених різниць використовують позначення  .