Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 12

a)	x	-1	0	1	b)	x	1	2	4
	y	3	2	5		y	3	4	6

19  Обчислити , знаючи значення  та .

20  Побудувати кусково-лінійну інтерполяцію функції  за вузлами –1, 0, 1.

21  Функція наближається на відрізку 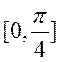 інтерполяційним многочленом за значеннями в точках 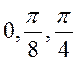. Оцінити похибку інтерполяції на цьому відрізку.

22  З яким постійним кроком h потрібно скласти таблицю функції  на відрізку 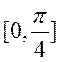, щоб похибка лінійної інтерполяції не перевищувала ?

23  Для таблично заданих функцій

a)	x	-1	0	1	2	b)	x	1	2	4	5
	y	3	2	5	1		y	3	4	6	5

              побудувати лінійний і параболічний  сплайни.

24 Функція y=y(x) задана таблицею своїх значень:

x	-1	0	1	2
y	1.8	2.4	2.2	2

Побудувати многочлени нульового й першого степенів, що наближають функцію за методом найменших квадратів. Обчислити величину середньоквадратичного відхилення. Побудувати на одному кресленні точковий графік функції й графіки многочленів.

25 Побудувати інтерполяційні многочлени у формі Лагранжа й Ньютона,  що наближають функцію y=y(x), задану таблицею своїх значень. Порівняти результати.

x	0	2	4
y	3	0	2

26 Функція у=y(x) задана таблицею своїх значень:

x	0	0.2	0.4	0.6	0.8	1
y	0.75	1.1	1.35	1.25	1.05	0.8

Запропонувати способи інтерполяції для знаходження значень функції в точках x=0.24,0.5, 0.96.

27 Відновити многочлен  за його значеннями:

	1	2	3
	2	8	16

28 Функція  задана таблицею своїх значень:

	0	1	2	3
	1	2	4	8

Обчислити наближено значення функції в точці  за допомогою інтерполяційного многочлена другого ступеня: а) у формі Лагранжа; б) у формі Ньютона (зі скінченними різницями). Оцінити похибку інтерполяції.

29 Функція 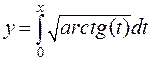 задана таблицею своїх   значень:

	0.6	0.8	1.0	1.2	1.4
	0.302	0.458	0.629	0.811	1.002

Обчислити приблизно значення функції в точці  за допомогою інтерполяційного многочлена у формі Ньютона (з розділеними різницями). Обчислити похибку інтерполяції.

30 Функція  задана таблицею своїх значень:

	0	1	2
	1	4	6

Побудувати природний інтерполяційний кубічний сплайн дефекту 1.

31 Відомо, що апроксимуюча функція має вигляд 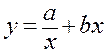, де a й b – невідомі параметри. Використовуючи метод найменших квадратів, визначити a й b, якщо відомо таблицю значень функції:

	0.1	0.2	0.5
	10.22	5.14	2.76

32 Вивести систему рівнянь для визначення коефіцієнтів a й b функції , що здійснює середньоквадратичну апроксимацію таблично заданої функції  y(x) в n+1 точках.  

33 Функція  наближається інтерполяційним многочленом за значеннями в точках x=0,,. Оцінити похибку інтерполяції на відрізку .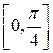

34 З яким кроком варто задати таблицю логарифмів на відрізку [1,10], щоб при квадратичній інтерполяції значення в проміжній точці відновлювалося з похибкою 0.001?