Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 3

Домовимося розміщувати таблиці розділених різниць у такий спосіб:

При   скінченні і розділені різниці пов'язані співвідношенням у вигляді

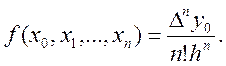
Розділені різниці порядку n від многочлена n-го степеня постійні, а різниці більш високого порядку дорівнюють нулю. Останнім зауваженням можна скористатися для виявлення помилок у таблицях многочленів чи функцій, близьких до них.     

За допомогою розділених різниць можна побудувати інтерполяційний многочлен Ньютона

  

  Варто зазначити, що при збільшенні кількості вузлів процес обчислення скінченних  та поділених різниць стає все більш обчислювально нестійким - похибка визначення скінченних різниць великого порядку різко зростає зі збільшенням порядку скінченної різниці. Тому метод Ньютона може бути застосований лише  для невеликої кількості вузлів.

5.2.3 Інтерполювання за Ермітом

У більш загальному випадку потрібно, щоб у вузлах інтерполяції збігалися не лише значення інтерполюючої функції і функції, яку необхідно інтерполювати, але й значення їхніх похідних до деякого порядку. У цьому випадку застосовують інтерполювання за Ермітом.

Інтерполяційним поліномом Ерміта -го порядку називають поліном  аргумента , який визначається з умов

;;

;;.;           

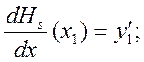
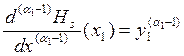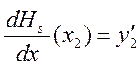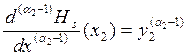.   .   .   .   .   .   .   .   .   .    .                     (5.17)

;;.;

.   .   .   .   .   .   .   .   .   .    .

;;.

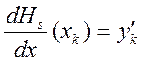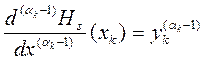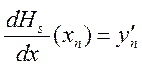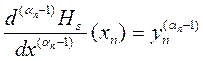Тут, як і раніше,  - кількість вузлів інтерполяції.

Якщо у вузлі    поліном і функція, яка інтерполюється, збігаються до похідної порядку , то число  називається кратністю вузла . При цьому .

Інтерполяційний поліном Ньютона (5.12) узагальнюється на випадок кратних вузлів таким чином:

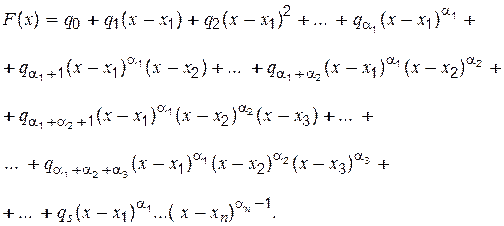 (5.18)

Інтерполювання за Ермітом зводиться до визначення  коефіцієнтів , , ...,   з умов (5.17).

5.2.4 Похибка інтерполяції та способи її зменшення

            Зафіксуємо точку x та визначимо похибку інтерполяції r_n(x)=f(x)-P_n(x). Нехай  та введемо функцію       g(s)=f(s)-P_n(s)-kw(s), де w(s)=(s-x₀)(s-x₁)…(s-x_n). При s=x_i, i=0,1,…,n, w(x_i)=0. Тому g(x_i)=0, бо f(x_i)=P_n(x_i). Виберемо деяку точку x¹x_i, i = 0,1,…,n та виберемо коефіцієнт k так, щоб g(x)=0. Тоді f(x)-P_n(x)-kw(x)=0; k=(f(x)-P_n(x))/w(x).

Враховуючи, що w⁽ⁿ⁺¹⁾(s) = (n+1)! та те, що g(s) має n+2 нулі на [a;b], то g'(s) має n+1 нуль, g''(s) має n нулів, …, g⁽ⁿ⁺¹⁾(s) має принаймні один нуль. Нехай це буде при s=x. Тоді

.

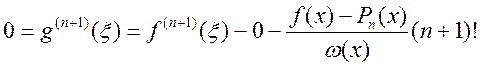Звідси отримуємо оцінку для похибки інтерполювання

.

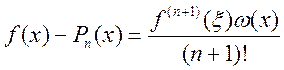Тоді оцінка для абсолютної похибки поліноміальної інтерполяційної формули  має вигляд

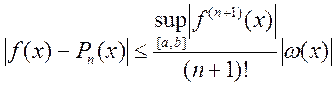.         (5.19)

Як бачимо з (5.19), похибка заміни функції  інтерполяційним многочленом залежить від вибору вузлів інтерполяції . Перш ніж перейти до питання про раціональний вибір вузлів інтерполяції, розглянемо деякі властивості одного з найважливіших і добре вивчених зараз класів спеціальних функцій – многочленів Чебишева першого роду, що часто використовуються для наближення функцій. Многочлен Чебишева  го степеня визначається за формулою

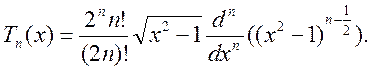     (5.20)

Для визначення многочленів Чебишева часто користуються тригонометричною формою запису

,          (5.21)

що приводить до таких самих виразів для , як і в (5.20).

Із тотожності 

при  маємо рекурентну формулу

.

Многочлен  має  коренів, які можна отримати, розв’язавши рівняння , або ;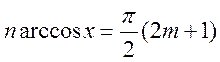

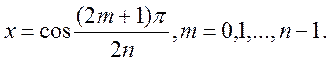         (5.22)

Як бачимо з (5.22), всі  коренів, що відповідають значенням  знаходяться на відрізку [-1,1], причому ці точки не рівновіддалені, а згущуються ближче до кінця даного відрізка. З формули (5.21) також очевидно, що на відрізку [-1,1]