Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 7

Вигляд граничних умов змінює деякі елементи матриці A, але в кожному разі вона залишається матрицею з діагональною перевагою. Розв’язок системи (5.35) із тридіагональною матрицею A може бути знайдений  методом прогонки.

Випадки використання кубічного сплайна

При побудові інтерполяційного кубічного сплайна найчастіше використовуються граничні (крайові) умови трьох типів. Вибір граничних (крайових) умов є однією з центральних проблем при інтерполяції функцій. Він особливо важливий за необхідності забезпечити високу точність апроксимації функції  сплайном  поблизу кінців відрізка . Граничні значення суттєво впливають на поведінку сплайна  поблизу точок а та b. Цей вплив швидко слабшає при відході від них.

Отже, якщо 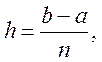  (), , то кубічний сплайн на цьому відрізку можна представити формулою

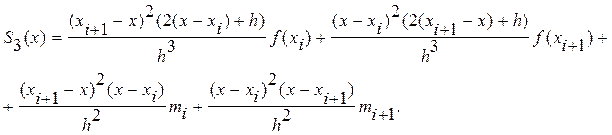Тут  . Для їх визначення  накладають умови неперервності другої похідної в точках  та обмеження на значення сплайна і його похідних на кінцях проміжку  - крайові умови. Тобто потрібна додаткова інформація про функцію, для якої є потреба в інтерполюванні.

Якщо на кінцях відрізка  відомі значення 1-ї похідної , то природно скористатися граничними (крайовими) умовами 1-го типу.

1  Граничні (крайові) умови 1-го типу. Якщо відомо, що , то для визначення  маємо систему рівнянь

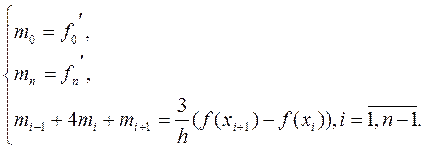(5.36)

Якщо на кінцях відрізка  відомі значення 2-ї похідної , то природно скористатися граничними (крайовими) умовами 2-го типу.

2  Граничні (крайові) умови 2-го типу. Якщо відомо

, то є система рівнянь

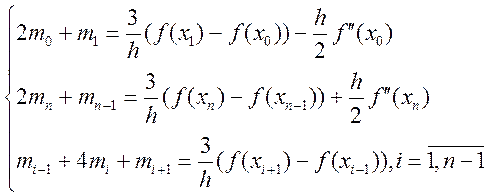 .     (5.37)

Якщо є можливість вибору між граничними (крайовими) умовами 1-го та 2-го типів, то перевагу потрібно надати умовам 1-го типу.

У випадку, коли ніякої додаткової інформації про поведінку апроксимованої функції немає, часто використовують так звані природні граничні (крайові) умови .

Однак варто мати на увазі, що при такому виборі граничних (крайових) умов точність апроксимації функції  сплайном  поблизу кінців відрізка  різко знижується. Іноді користуються граничними (крайовими) умовами 1-го або 2-го типу, але не з точними значеннями відповідних похідних, а з їх різницевими апроксимаціями. Точність такого підходу невисока.

  Практичний досвід розрахунків показує, що в такій ситуації найбільш доцільним є вибір природних граничних ( крайових) умов. Якщо  - періодична функція, то потрібно зупинитися на граничних (крайових) умовах 3-го типу.

3  Граничні (крайові) умови 3-го типу. Якщо  - періодична функція , то  і система рівнянь має вигляд

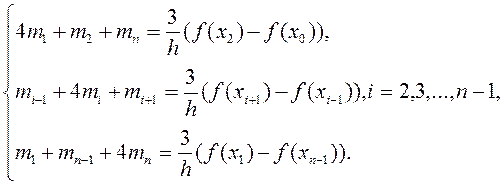 . (5.38)

Приклад реалізації алгоритмів інтерполяції функцій на псевдокоді

//розв’язує СЛАР методом Гауса

//M – матриця системи і вільні члени

//X – вектор відповідей

//n – кількість невідомих

linequ(M,n,e,X): 

//доступна в модулі naz.pas

end

//X – значення аргумента

//Y – значення функції

//xi – значення аргумента, для якого потрібно знайти значення

//     функції

//h – крок

//змінні DY, D2Y і т.д. – скінченні різниці

//змінні SDY, SD2Y і т.д. – розділені різниці

//відшукуємо значення інтерполюючого многочлена при x=xi

Find_PX(X,Y,n,h):

1  n:=X.length;

2  for i:=1 to n do

3   DY[i]:=Y[i+1]-Y[i]

4  done

5  for i:=1 to (n-1) do

6   D2Y[i]:=DY[i+1]-DY[i]

7  done

8  for i:=1 to (n-2) do

9   D3Y[i]:=D2Y[i+1]-D2Y[i]

10  done

11  for i:=1 to (n-3) do

12   D4Y[i]:=D3Y[i+1]-D3Y[i]

13  done

14  for i:=1 to n do

15   SDY[i]:=Y[i+1]-Y[i]/(X[i+1]-X[i])

16  done

17  for i:=1 to (n-1) do

18  D2Y[i]:=SDY[i+1]-SDY[i]/(X[i+2]-X[i])

19  done

20  for i:=1 to (n-2) do

21  D3Y[i]:=SD2Y[i+1]-SD2Y[i]/(X[i+3]-X[i])

22  done

23  for i:=1 to (n-3) do

24  D4Y[i]:=SD3Y[i+1]-SD3Y[i]/(X[i+4]-X[i])

25  done