Нехай функція f(x) – неперервна на відрізку [a,b], на кінцях його набуває значень різних знаків, тобто f(a)*f(b)<0, похідна f’(x) зберігає на цьому відрізку знак. Виходить, усередині цього відрізка міститься корінь.
Рівняння ![]() має корінь на
відрізку [0.5..1], тому що:
має корінь на
відрізку [0.5..1], тому що:
f(0,5) = 0.3678794412 > 0
f(1) = − 0.8646647168 > 0
f(0,5)*f(1) < 0
Методом половинного поділу звузимо цей інтервал до [0.5..0.75]. Теорема 1 виконується й для нього (на ньому також буде корінь).
Використаємо метод простої ітерації. Перевірка
достатньої умови збіжності для методу простої ітерації: для цього замінимо
f(x)=0 на еквівалентне йому рівняння в вигляді х=φ(х), в нашому випадку 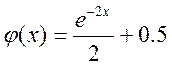 ; знайдемо похідну
цього виразу ─
; знайдемо похідну
цього виразу ─ ![]()
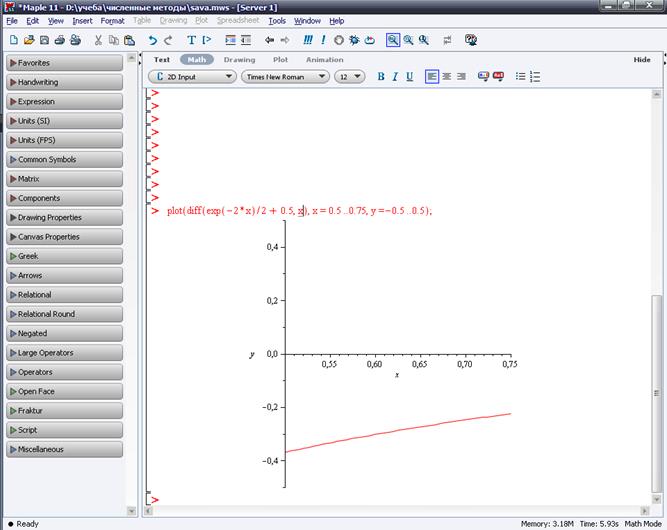
Перевіримо на інтервалі [0.5..0,75] (графік 1).
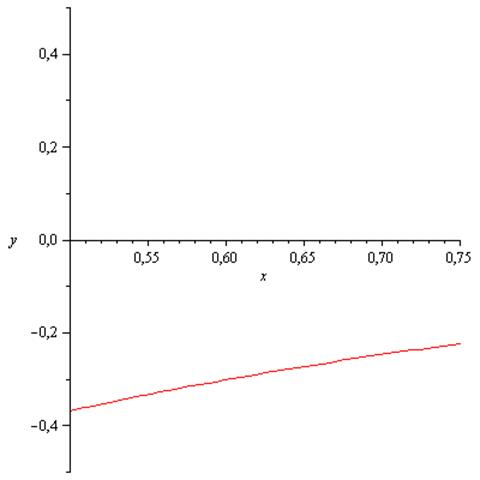
Графік 1
За допомогою графіку можна побачити, що на
розглянутому інтервалі умова збіжності для методу простої ітерації виконується. Таким чином можна використовувати метод простої
ітерації для розв'язання нелінійного рівняння ![]() .
.
Вибираємо початкове наближення x0. Виберемо х0 = 0,5.
#include <stdio.h>
#include <math.h>
#include <conio.h>
void main()
{ double x0,x,e;
clrscr();
scanf("%lf%lf",&x,&e);
do {
x0=x;
x=exp(-2*x0)/2+0.5;
} while (fabs(x0-x)>e);
printf("%f\n",x); }
Де:
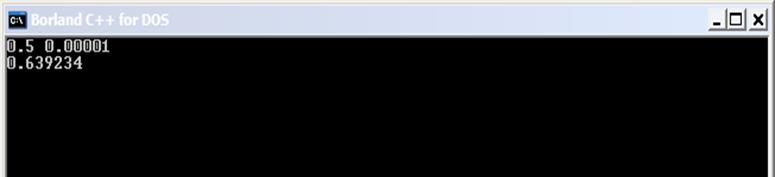
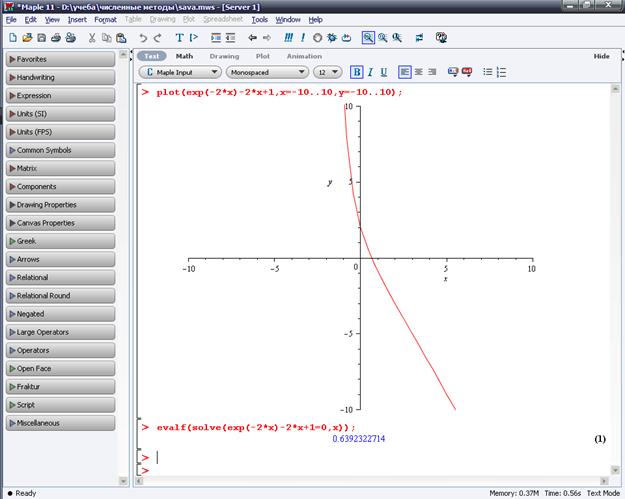
Знайдемо корінь рівняння ![]() в Maple та за допомогою програми, яка була
створена в процесі виконання лабораторної роботи. Створена програма точно
знаходить корінь з заданою точністю.
в Maple та за допомогою програми, яка була
створена в процесі виконання лабораторної роботи. Створена програма точно
знаходить корінь з заданою точністю.
Значення в Maple: 0.6392322714.
Значення в програмі з точністю 10-5: 0.639234
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.