Метод найменших квадратів (Лабораторна робота № 5)

Міністерство освіти і науки України

Сумський державний університет

Кафедра інформатики

Лабораторна робота №5

з дисципліни

«Чисельні методи»

на тему:

«Метод найменших квадратів»

Варіант 10

Підготував

студент ІН-91

Приходько М. С.

Перевірила

Назаренко Л.Д.

Суми 2011

1.  Умова задачі:

 Аналітичний опис результатів 9експериментів, у кожному з яких на вхід системи подається значення параметра Х, а на виході реєструється реакція У.

1 Вибрати вид функції.

2 Методом найменших квадратів знайти коефіцієнти.

2	X	0,75  0,78   0,83  0,88  0,93  0,98  1,03  1,21  1,45
	Y	10     32,5    47,7  46,1    90   91    95,6   98,2  102

2.  Математичне обґрунтування та вибір алгоритму розв’язання задачі

За результатами n експериментів необхідно одержати залежність , що може показати,як у середньому y залежить від x. Таке рівняння називають рівнянням регресії.

Потрібно підібрати таку аналітичну залежність у= ,яка якнайкраще в умовах якогось заданого критерію описувала б отримані результати.

При розв'язанні даної задачі найбільшого поширення набув метод найменших квадратів (МНК). Цим методом підбирається таке рівняння y= , при якому сума квадратів відхилень експериментальных значень від розрахункових , отриманих після підстановки x=x у це рівняння, набувала б мінімального значення. Аналітично ця вимога має вигляд

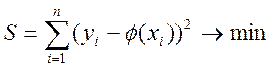
Припустимо відомо ,що між x і y існує лінійна залежність y= Невідомі коефіцієнти  знайдемо з необхідної умови екстремуму функції

.

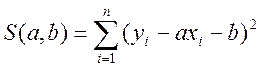У результаті одержимо два рівняння:

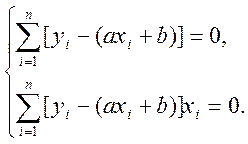
Розв’язуючи систему ,знаходимо a і b , що при заданому вигляді рівняння регресії забезпечують мінімум S :

a= ,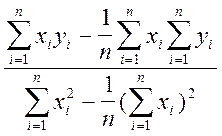

b=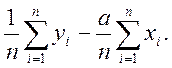

Вибір вигляду регресійної залежності можна здійснити за таблицею. Для цього за вихідними даними обчислюють середні значення х_ср та у_ср :

,  ,  ,

    .

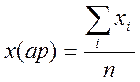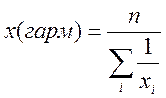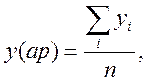
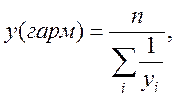
 Величина обчислюється так:

1) якщо  збігається з одним із вихідних , то ;

2) якщо  знаходиться між  і ,  знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли  і , за формулою

.

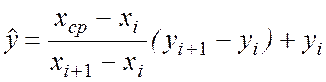Вибір рівняння регресії здійснюється шляхом пошуку мінімального значення виразу 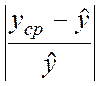 і відповідної йому функції, використовуючи таблицю:

N					Вигляд  функції
1	X(ар)	Y(ар)			у=а0+a1x
2	X(га)	Y(ар)			y=a0+a1lnx
3	X(ге)	Y(ар)			у=а0+а1/x
4	X(ар)	Y(ге)			y=a0a1x
5	X(ге)	Y(ге)			y=a0xa1
6	X(га)	Y(ге)			y=exp(a0+a1/x)
7	X(ар)	Y(га)			y=1/(a0+a1x)
8	X(ге)	Y(га)			y=1/(a0+a1lnx)
9	X(га)	Y(га)			y=x/(a0+a1x)

Обчислимо середні значення х_ср та у_ср за наведеними вище формулами:

x(ар)	х(гарм)	х(геом)	y(ар)	y(гарм)	y(геом)
0,98	0,943473	0,9617147	68,122222	39,827739	56,21336

Визначимо рівень регресії, як показано в таблиці 1:

Номер п/п					Вигляд функції
1	0,982222	68,12222	91,20444	0,253082208	у=а0+a1x
2	0,961715	68,12222	90,63429	0,248383594	y=a0+a1lnx
3	0,943473	68,12222	90,26947	0,24534592	у=а0+а1/x
4	0,982222	56,21336	91,20444	0,383655441	y=a0a1x
5	0,961715	56,21336	90,63429	0,379778219	y=a0xa1
6	0,943473	56,21336	90,26947	0,37727158	y=exp(a0+a1/x)
7	0,982222	39,82774	91,20444	0,563313617	y=1/(a0+a1x)
8	0,961715	39,82774	90,63429	0,560566566	y=1/(a0+a1lnx)
9	0,943473	39,82774	90,26947	0,558790587	y=x/(a0+a1x)

Очевидно, що рівняння регресії матиме вигляд y=a₀+a₁lnx.Оскільки функція нелінійна, потрібно її лінеаризувати. Запишемо її у вигляді y=a₀+a₁k., k=lnx. Знайдемо коефіцієнти а0, a1 апроксимуючої функції за формулами:

a₁=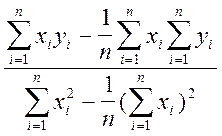 , a₁=-144,855

94

a₀ 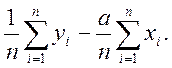 = ,  a₀  =221,656

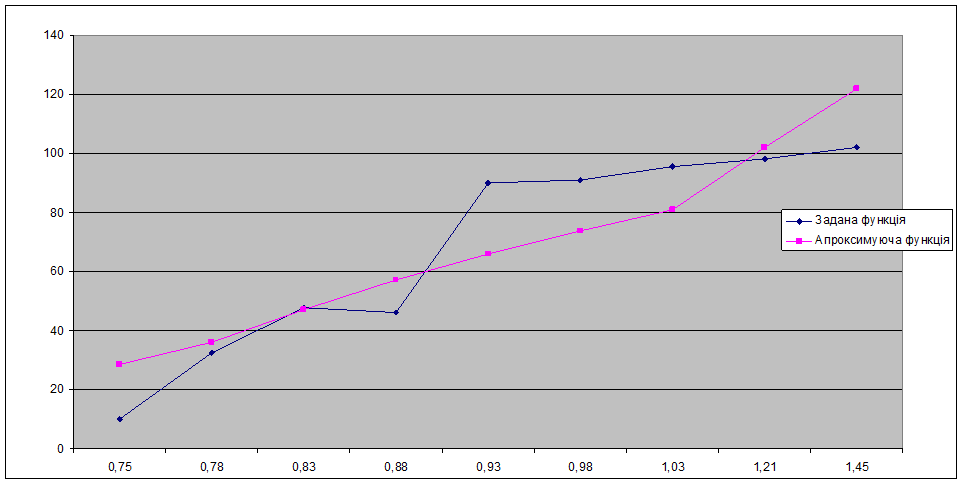
Отже апроксимуюча функція матиме вигляд у=221,656-144,855/x

Апроксимуюча та базова функції :

2. Програмна реалізація:

#include<stdio.h>

#include<conio.h>

#include<math.h>

#define N 9

float A1 (float x[N],float y[N])

{

float sumxy=0, sumx=0,sumy=0,sumx2=0,a1;

int i;

for (i=0;i<N;i++)

 {

              sumxy+=(x[i]*y[i]);

              sumx+=x[i];

              sumy+=y[i];

              sumx2+=(x[i]*x[i]);

 }

              a1=(sumxy-(1.0/N)*sumx*sumy)/(sumx2-(1.0/N)*sumx*sumx);

return a1;

}

float A0(float x[N],float y[N],float a1)

{

float sumx=0,sumy=0,a0;

int i;

for (i=0;i<N;i++)

 {

              sumx+=x[i];

              sumy+=y[i];

 }

              a0=(1.0/N)*(sumy-a1*sumx);

return a0;

}

void main()

{

float x[N], y[N],my[N], lx[N], ly[N], x1[N], y1[N];

float min, a0, a1,xar=0,xga=0,xge=1,yar=0,yga=0,yge=1,yy;

int i,k=0;

FILE *p2, *p3;

clrscr();

p2=fopen("znx.txt","r");

p3=fopen("zny.txt","r");

for(i=0;i<N;i++)

 {

                            fscanf(p2,"%f", &x[i]);

                            fscanf(p3,"%f ",&y[i]);