Метод найменших квадратів (Лабораторна робота № 5), страница 3

                                                                       a0=A0(x,y,a1);

                                                                       printf("\ny=%f+(%f)x",a0,a1);

                            break;

                             case 2:

                            a1=A1(lx,y);

                            a0=A0(lx,y,a1);

                                                                       printf("\ny=%f+(%f)lnx",a0,a1);

                            break;

                             case 3:

                            a1=A1(x1,y);

                            a0=A0(x1,y,a1);

                                                                       printf("\ny=%f+(%f)/x",a0,a1);

                            break;

                             case 4:

                            a1=exp(A1(x,ly));

                            a0=exp(A0(x,ly,log(a1)));

                                                                       printf("\ny=%f*(%f)^x",a0,a1);

                            break;

                             case 5:

                            a1=A1(lx,ly);

                            a0=exp(A0(lx,ly,a1));

                                                                       printf("\ny=%f*x^(%f)",a0,a1);

                            break;

                             case 6:

                            a1=A1(x1,ly);

                            a0=A0(x1,ly,a1);

                                                                       printf("\ny=exp(%f+(%f)/x)",a0,a1);

                            break;

                             case 7:

                            a1=A1(x,y1);

                            a0=A0(x,y1,a1);

                                                                       printf("\ny=1/(%f+(%f)x)",a0,a1);

                            break;

                             case 8:

                            a1=A1(lx,y1);

                            a0=A0(lx,y1,a1);

                                                                       printf("\ny=1/(%f+(%f)/x)",a0,a1);

                            break;

                             case 9:

                            a0=A1(x1,y1);

                            a1=A0(x1,y1,a0);

                                                                       printf("\ny=x/(%f+(%f)x)",a0,a1);

                            break;

}

getch();}

3. Пакетна реалізація алгоритму

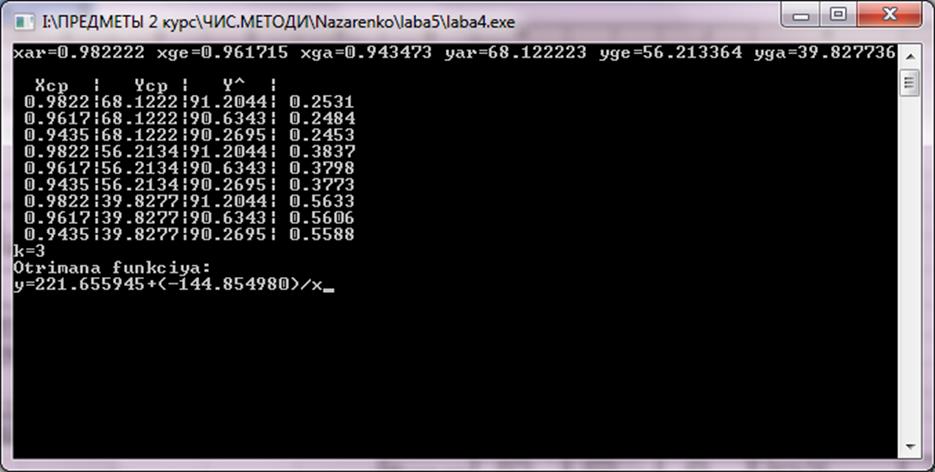
Пакетна реалізація алгоритму здійснена засобами Excel, де було побудовано два графіка для порівняння результатів, а саме наскільки близька апроксимуюча функція, до функції заданої таблично.

4. Висновок:

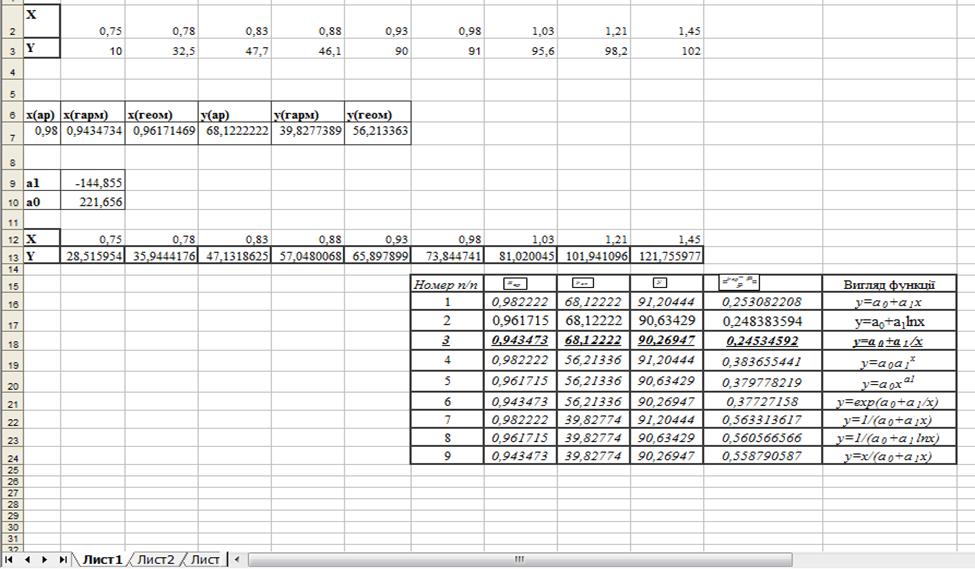
У даній лабораторній роботі була знайдена апроксимуюча функція для зданих вхідних значень x та y. На графіках, побудованих в Excel, видно наскільки отримана функція близька до заданих значень. Результати, отримані програмно та пакетно збігаються.