Методом Зейделя розв’язати систему лінійних алгебраїчних рівнянь вигляду АХ=В із точністю до 0,0001.
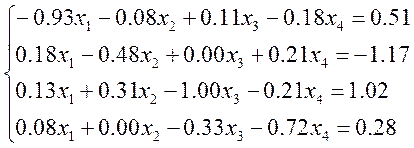
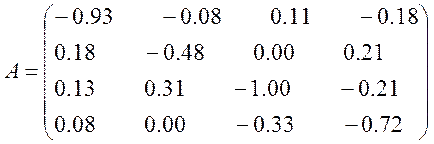
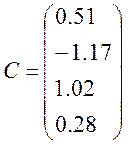
Перевіримо достатню умову збіжності ітераційного процесу для метода Зейделя. Вона полягає в тому, що абсолютна величина коефіцієнта, який стоїть на головній діагоналі матриці А повинна бути більшою за суму абсолютних величин інших чисел цього рядка матриці А.
Перевіримо цю умову.
Для
першого рядка маємо
|-0.93|>|-0.08|+|0.11|+|-0.18|=0.37 - умова
виконується.
Для
другого рядка маємо
|-0.48|>|0.18|+|-0.00|+|0.21|=0.39
-
умова виконується.
Для
третього рядка маємо
|-1.00|>|0.13|+|0.31|+|-0.21|=0.65 - умова виконується.
Для
четвертого рядка маємо
|-0.72|>|0.08|+|0.00|+|-0.33|=0.41 - умова
виконується.
Використаємо
метод Зейделя. Розглянемо тепер систему AX=C з 4 рівнянь із 4
невідомими, припускаючи, що діагональні коефіцієнти aii
відмінні від нуля для всіх i. Перетворимо вихідну систему вигляду Aх=C
до вигляду х=Bх+D, де B=[bij] - квадратна
матриця порядку n: ![]()
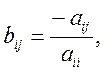
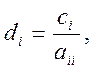
![]() .У цьому випадку ітераційний процес методу
Зейделя має вигляд:
.У цьому випадку ітераційний процес методу
Зейделя має вигляд:
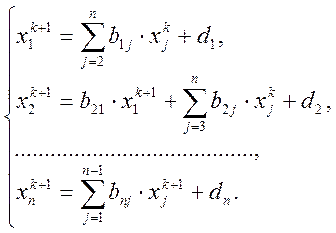 (3.5)
(3.5)
Обчислення проводимо до тих пір, поки
![]()
тобто коли наближені
розв’язки ![]() і
і ![]()
![]() стануть досить
близькими і
стануть досить
близькими і 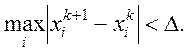 Величина ∆ пов'язана з точністю
ε розв’язання системи
співвідношенням
Величина ∆ пов'язана з точністю
ε розв’язання системи
співвідношенням 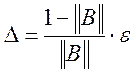 , де
, де![]() - норма
матриці з коефіцієнтів при невідомих у правих частинах рівнянь перетвореної
системи: х=Bх+D. Норма
матриці може бути визначена по різному, наприклад, як
- норма
матриці з коефіцієнтів при невідомих у правих частинах рівнянь перетвореної
системи: х=Bх+D. Норма
матриці може бути визначена по різному, наприклад, як
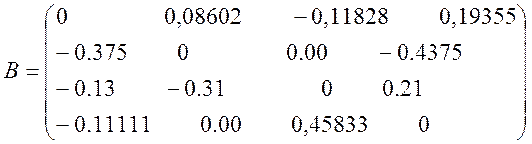
Норму ![]() обчислимо
за допомогою формули
обчислимо
за допомогою формули 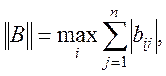
при і=1: 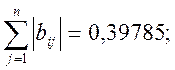
при і=2: 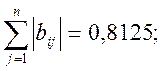
при і=3: 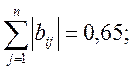
при і=4: 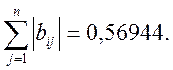
Таким чином норма матриці В дорівнює 0.8125.
За початкове наближення беремо: х10 = 0; х20 = 0; х30 = 0; х40 = 0.
#include <stdio.h>
#include <conio.h>
#include <math.h>
float x0[4],x[4],e=0.0001,normB=0.8125,delta,n,n1,m[4][5];
int i;
void nul (float *a,float *b)
{ for(i=0;i<4;i++) a[i]=b[i]; }
float eqal(float a,float b,float c,float d,float e, float x1, float x2, float x3)
{ return (a-b*x1-c*x2-d*x3)/e; }
void main()
{
clrscr();
m[0][0]=-0.93; m[0][1]=-0.08; m[0][2]=0.11; m[0][3]=0.18; m[0][4]=0.51;
m[1][0]=0.18; m[1][1]=-0.48; m[1][2]=0; m[1][3]=0.21; m[1][4]=-1.17;
m[2][0]=0.13; m[2][1]=0.31; m[2][2]=-1; m[2][3]=-0.21; m[2][4]=1.02;
m[3][0]=0.08; m[3][1]=0; m[3][2]=-0.33; m[3][3]=-0.72; m[3][4]=0.28;
puts("x01= x02= x03= x04= ");
for (i=0;i<4;i++)
scanf("%f",&x[i]);
delta=((1-normB)*e)/normB;
printf("delta=%f\n",delta);
do{
n=sqrt(pow(x0[0],2)+pow(x0[1],2)+pow(x0[2],2));
nul(x0,x);
x[0]=eqal(m[0][4],m[0][1],m[0][2],m[0][3],m[0][0],x[1],x[2],x[3]);
x[1]=eqal(m[1][4],m[1][0],m[1][2],m[1][3],m[1][1],x[0],x[2],x[3]);
x[2]=eqal(m[2][4],m[2][0],m[2][1],m[2][3],m[2][2],x[0],x[1],x[3]);
x[3]=eqal(m[3][4],m[3][0],m[3][1],m[3][2],m[3][3],x[0],x[1],x[2]);
n1=sqrt(pow(x[0],2)+pow(x[1],2)+pow(x[2],2));
} while((n1-n)>delta);
for (i=0;i<4;i++)
printf("x%d=%f\n",i+1,x[i]);
}

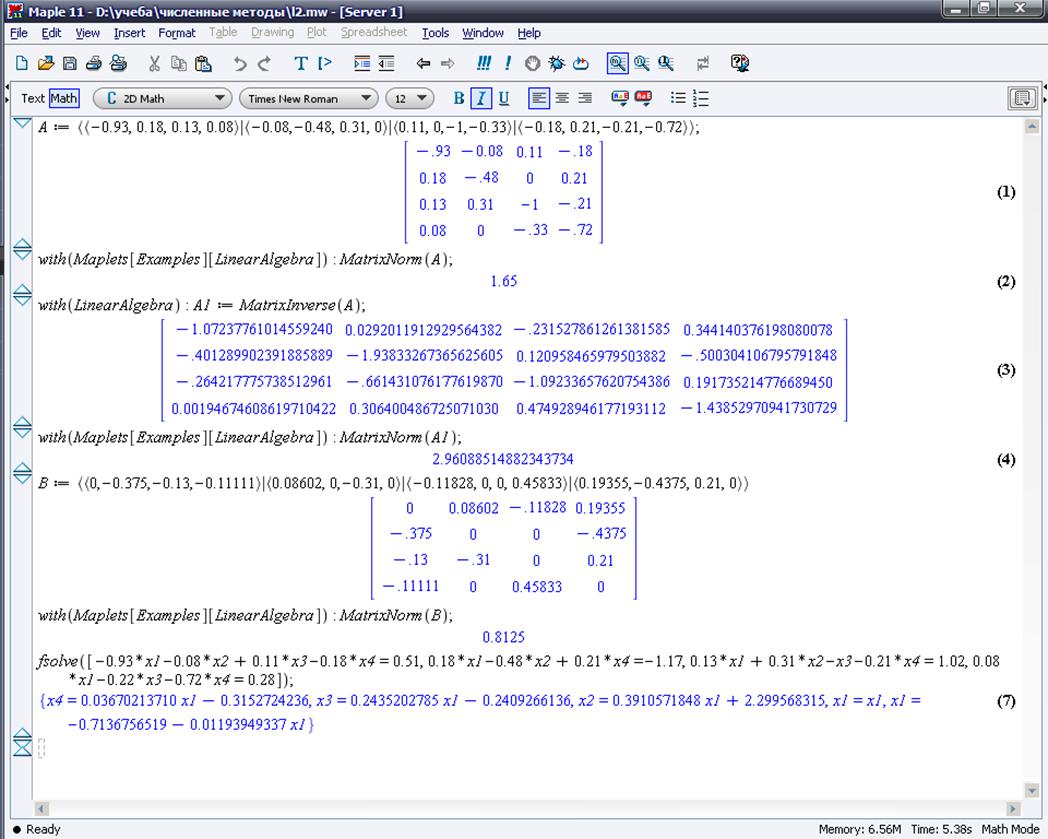
Визначимо міру обумовленості та оцінимо вплив вхідних даних на результат. Знайдемо норму матриць А, А-1, В.
||А||=1.65
||А-1||=2.96088514882343734
||В||=0.8125
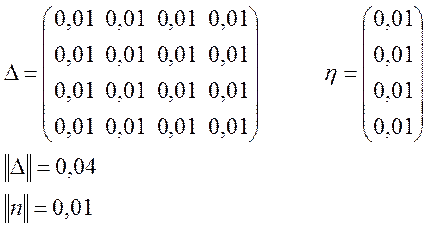
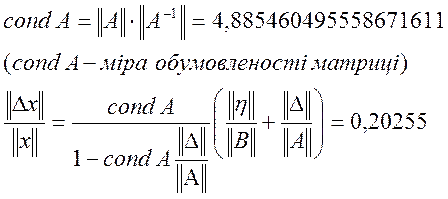
Тобто, похибка вхідних даних складає 20,255%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.