Дифференциальные уравнения. Часть I: Методические указания к выполнению расчетно-графической работы

I. Основные типы дифференциальных уравнений и методы их решения

Уравнения, разрешенные относительно
производной

Определение. Дифференциальное уравнение вида

                                            (1)

называется дифференциальным уравнением, разрешенным относительно производной.

Определение. Общее решение дифференциального уравнения имеет вид , где  – произвольная постоянная. Выбирая конкретное значение константы , получаем частное решение.

Определение. Областью задания уравнения (1) будем называть область задания функции .

Определение Областью определения уравнения (1) будем называть объединение областей  задания функции  и функции .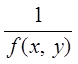

Определение. Дифференциальное уравнение  (1) с дополнительным условием

                                             (2)

называется задачей Коши или начальной задачей, условие (2) называется начальным условием или условием Коши.

Теорема существования и единственности. Пусть в некотором прямоугольнике  функция  непрерывна по совокупности переменных  и  и удовлетворяет условию Липшица  по аргументу , где   – произвольные точки из прямоугольника ;  – константа Липшица. Тогда на сегменте , где 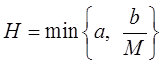,  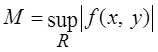существует и единственно решение задачи Коши (1) – (2).

Замечание. Если выполнены все условия теоремы существования и единственности, кроме условия Липшица, то решение задачи (1) – (2) существует, но, вообще говоря, может быть  не единственным.

Определение. Если через точку  проходит неединственная интегральная кривая (нарушены условия единственности решения) или не проходит ни одной интегральной кривой (нарушены условия  существования решения), то такая точка называется особой. Линии, состоящие из особых точек, называются особыми линиями.

1. Уравнения с разделяющимися переменными имеют вид

.

Эти уравнения приводятся к виду уравнений с разделенными переменными:

.

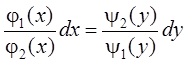Проинтегрировав соотношение, получаем общее решение дифференциального уравнения (ДУ):

,

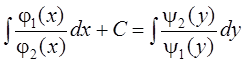здесь C – произвольная постоянная.

Замечание. При делении на функции  и  возможна потеря частных решений, обращающих эти функции в ноль.

2. Уравнения, приводящиеся к уравнениям с разделяющимися переменными:

,

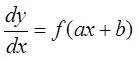где a, b – константы. Сделав замену переменных , получаем  ДУ с разделяющимися переменными: .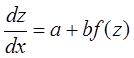

3. Однородные дифференциальные уравнения:

.

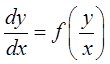Замена переменных 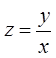 приводит уравнение к виду .

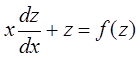4. Уравнения, приводящиеся к однородным ДУ:

.

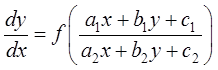Замена переменных: перенос начала координат в точку  пересечения прямых  и , – . Новые переменные: .

После замены переменных уравнение примет вид

.

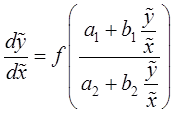Если прямые  и  параллельны, то ДУ приводится к уравнению типа 2.

5. Линейные дифференциальные уравнения первого порядка:

.

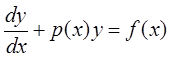Уравнения такого типа решаются методом вариации постоянной [1]:

1) решение однородного линейного ДУ первого порядка: 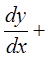 . Общее решение однородного ДУ имеет вид  , где C – произвольная постоянная;

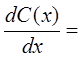
2) полагаем в решении однородного линейного ДУ первого порядка  функцией переменной x и определяем эту функцию таким образом, чтобы решение  было решением неоднородного ДУ. Подставляя решение в исходное неоднородное ДУ, получаем уравнение для определения функции :  . Общее решение неоднородного ДУ имеет вид: , где  – произвольная постоянная.

6. Уравнение Бернулли:

.

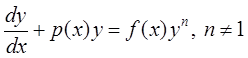Замена переменных  приводит уравнение Бернулли к виду линейного уравнения первого порядка.

7. Уравнение Риккати:

.

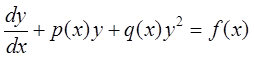Уравнения этого типа в общем виде не интегрируются, но если известно хотя бы одно частное решение уравнения, то заменой  ( – частное решение,  – новая неизвестная функция) уравнение Риккати приводится к уравнению Бернулли.

8. Уравнения в полных дифференциалах:

,

где 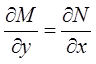, тогда уравнение представляет собой полный дифференциал некоторой функции : . Решение этого уравнения – функция , где C – произвольная постоянная. Будем искать решение ДУ в полных дифференциалах в виде . Тогда

.

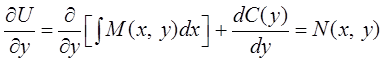Из последнего соотношения определяется функция .

Уравнения, не разрешенные относительно
производной