Краевые задачи.
Задача о стационарном распределение тепла в стержне, на концах которого поддерживается постоянная температура.
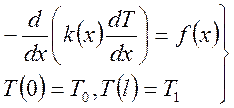 (1)
(1)
![]()
![]() - источник тепловыделения;
- источник тепловыделения; ![]() - коэффициент теплопроводности;
- коэффициент теплопроводности; ![]() - температура.
- температура.
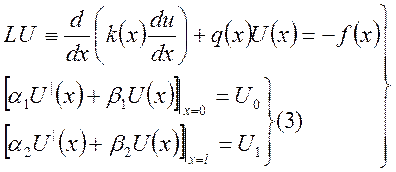 (2)
(2)
Определение.
В (3) ![]() - это числа, не обращающиеся в ноль
одновременно, и выполняется условие
- это числа, не обращающиеся в ноль
одновременно, и выполняется условие ![]() . Если
. Если ![]() , то получаем краевые условия первого рода,
так называемые условия Дирихле. Если
, то получаем краевые условия первого рода,
так называемые условия Дирихле. Если ![]() , то получим краевые условия второго рода
или условия Неймана. Если
, то получим краевые условия второго рода
или условия Неймана. Если ![]() и
и
![]() одновременно, то получим краевые
условия третьего рода.
одновременно, то получим краевые
условия третьего рода.
Определение.
Однородная краевая задача – это задачи (2) и (3) тогда, когда ![]() . Однородная краевая задача всегда имеет
тривиальное решение, но может иметь и нетривиальное решение. Частный случай
однородной краевой задачи – это задача на собственные значения,
она состоит в определение параметров входящих в ДУ, при которых существует
нетривиальное решение однородной задачи.
. Однородная краевая задача всегда имеет
тривиальное решение, но может иметь и нетривиальное решение. Частный случай
однородной краевой задачи – это задача на собственные значения,
она состоит в определение параметров входящих в ДУ, при которых существует
нетривиальное решение однородной задачи.
Характерная задача на собственные значения – это задача определения
параметра ![]() , при котором существует нетривиальное
решение на интервале
, при котором существует нетривиальное
решение на интервале ![]() задачи:
задачи:
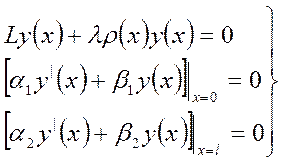 (4)
(4)
В этой
формуле оператор L – это
линейный дифференциальный оператор, такой же как в формуле (2); ![]() - это заданная функция, непрерывная на интервале
- это заданная функция, непрерывная на интервале
![]() ;
; ![]() -
заданные константы.
-
заданные константы.
Определение.
Значения параметра ![]() , при которых задача (4) имеет
нетривиальное решение, называются собственными значениями, а
соответствующие нетривиальные решения задачи (4) – собственными функциями
этой краевой задачи. Сама задача (4) называется задачей Штурма-Лиувилля.
, при которых задача (4) имеет
нетривиальное решение, называются собственными значениями, а
соответствующие нетривиальные решения задачи (4) – собственными функциями
этой краевой задачи. Сама задача (4) называется задачей Штурма-Лиувилля.
Свойства собственных функций этой задачи:
1.)
существует счетное множество собственных значений ![]() и соответствующих им собственных функций,
то есть
и соответствующих им собственных функций,
то есть ![]() . Все собственные значения задачи (4) можно
упорядочить по возрастанию их абсолютной величины:
. Все собственные значения задачи (4) можно
упорядочить по возрастанию их абсолютной величины: ![]()
2.) каждому собственному значению соответствует, с точностью до постоянной, только одна собственная функция. Ранг собственных значений равен единице.
3.)
в случае краевых условий Дирихле ( y(0)=y(l)=0 ) и при выполнение
следующих ограничений ![]() (из
формулы (2)), все собственные значения задачи (4) будут строго положительны:
(из
формулы (2)), все собственные значения задачи (4) будут строго положительны: ![]() .
.
Теорема о
разложимости Стеклова. Если функция f(x) (правая часть) непрерывна и дважды дифференцируема на
отрезке ![]() и удовлетворяет однородным краевым
условиям типа (4), то эта функция может быть представлена в виде абсолютно и
равномерно сходящегося ряда на интервале
и удовлетворяет однородным краевым
условиям типа (4), то эта функция может быть представлена в виде абсолютно и
равномерно сходящегося ряда на интервале ![]() по
собственным функциям
по
собственным функциям ![]() задачи (4), то есть функция
может быть представлена в виде:
задачи (4), то есть функция
может быть представлена в виде:
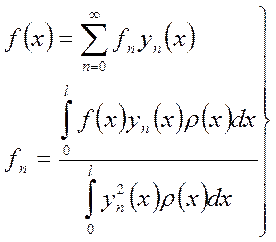 (5)
(5)
Замечание. Если дана неоднородная краевая задача с однородными краевыми условиями и правая часть f дифференциального уравнения – дважды непрерывно-дифференцируемая функция, то искать решение этой неоднородной задачи можно в виде (5).
Пример: 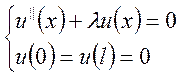
![]() ;
; ![]() ;
; 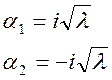
![]()
![]()
![]()
![]()
![]()
![]()
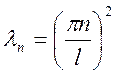
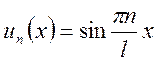
Решение краевых задач с помощью функции Грина.
Пусть дано
уравнение 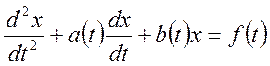 (1)
(1)
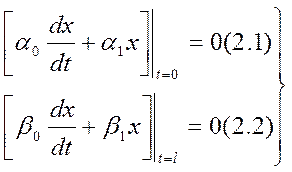 (2)
(2)
И пусть краевая задача имеет единственное решение. Рассмотрим однородное уравнение, соответствующее уравнению (1):
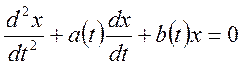 (3)
(3)
Пусть ![]() - это нетривиальное решение задачи (3),
удовлетворяющее краевому условию (2.1);
- это нетривиальное решение задачи (3),
удовлетворяющее краевому условию (2.1); ![]()
![]() - нетривиальное решение задачи (3),
удовлетворяющее краевому условию (2.2). Предположим, что
- нетривиальное решение задачи (3),
удовлетворяющее краевому условию (2.2). Предположим, что ![]() не удовлетворяет краевому условию (2.2), а
не удовлетворяет краевому условию (2.2), а
![]() - краевому условию (2.1).
- краевому условию (2.1).
Это
выполняется, так как если бы решение ![]() удовлетворяло условию
(2.2), то
удовлетворяло условию
(2.2), то ![]() тоже бы ему удовлетворяло, а значит
тоже бы ему удовлетворяло, а значит ![]() было бы решением задачи (3) с краевыми
условиями (2), а мы решили, что у нее единственное решение => противоречие.
было бы решением задачи (3) с краевыми
условиями (2), а мы решили, что у нее единственное решение => противоречие.
Таким
образом: 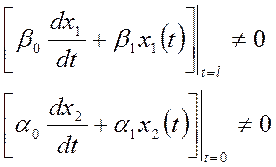 (4)
(4)
Решения ![]() и
и ![]() линейно
не зависимы, то есть если бы они были пропорциональны (линейно зависимы), то
удовлетворяли бы одним и тем же краевым условиям, что не возможно.
линейно
не зависимы, то есть если бы они были пропорциональны (линейно зависимы), то
удовлетворяли бы одним и тем же краевым условиям, что не возможно.
Раз у нас есть два линейно независимых решения, то решение неоднородной задачи (1-2) будем искать методом вариации постоянных.
![]() (5)
(5)
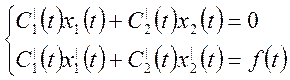
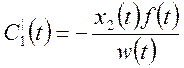 (6)
(6)
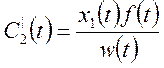 (7)
(7)
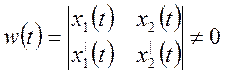
![]() , так
как
, так
как ![]() ,
, ![]() -
линейно независимы.
-
линейно независимы.
Проинтегрируем (6) и (7):
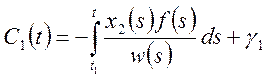
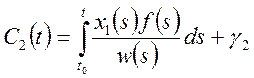
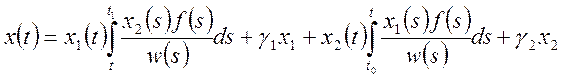 (8)
(8)
Проинтегрируем
(8) по t и получим выражение для ![]() ; подставим полученное соотношение в
краевые условия (2) и учтем, что
; подставим полученное соотношение в
краевые условия (2) и учтем, что ![]() удовлетворяет краевым
условиям (2.1), а
удовлетворяет краевым
условиям (2.1), а ![]() - краевым условиям (2.2).
- краевым условиям (2.2).
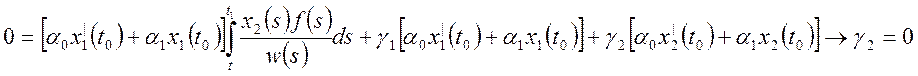
![]()
Подставим
другие краевые условия и получим, что ![]() .
.
Таким
образом 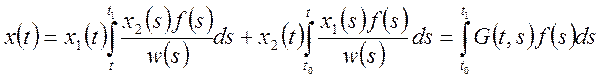 (9)
(9)
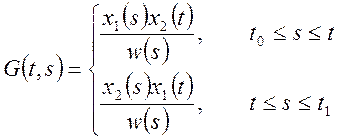 (10)
(10)
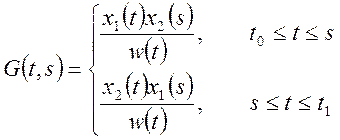
G(t,s) – функция
Грина для краевой задачи (1-2), если она определена, то решение краевой
задачи (1-2) определяется формулой (9). Для функции Грина определяются только
решения ![]() и
и ![]() -
линейно независимые и не зависящие от правой части f(x).
-
линейно независимые и не зависящие от правой части f(x).
При фиксированном s функция Грина обладает следующими свойствами:
1.) при функция Грина удовлетворяет однородному уравнению (3).
2.)
При ![]() функция Грина удовлетворяет краевым
условиям (2).
функция Грина удовлетворяет краевым
условиям (2).
3.)
При ![]() функция Грина непрерывна.
функция Грина непрерывна.
4.)
При ![]() производная функции Грина
производная функции Грина ![]() претерпевает единичный скачек, те есть
претерпевает единичный скачек, те есть
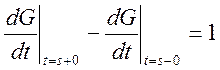 .
.
Доказательство получим исходя из соотношения (10).
Пример.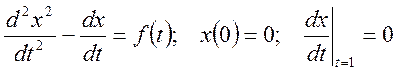
![]()
![]()
![]()
![]()
1.)
![]()
![]()
2.)
![]()
![]()
![]()
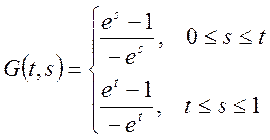
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.