Решение краевых задач конечно-разностными методами (Лабораторная работа № 2)

Министерство Образования и Науки РФ

Новосибирский Государственный Технический Университет

Кафедра прикладной математики и информатики

Лабораторная работа №2 по дисциплине

 «Дифференциальные уравнения» на тему:

Решение краевых задач конечно-разностными методами

Факультет:           ПМИ
Группа:                 ПМ-72
Студенты:             Щеголев В. С.

                              Чернов А. К.

Преподаватели:    Иткина Н.Б.

                              Баландин М.Ю.   

Новосибирск

 2009г.

1)  Цель работы:

Для краевой задачи, описывающей процесс стационарной одномерной теплопроводности, построить консервативную разностную схему, оценить порядок аппроксимации, устойчивость и сходимость.

2) Задание:

Построить консервативную схему для линейного уравнения теплопроводности:

  с коэффициентами 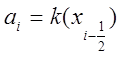,  с  краевыми

условиями третьего  и второго рода.

3)Построение схемы:

Пусть дано стационарное одномерное уравнение теплопроводности:

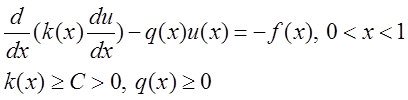
с третьими краевыми условиями: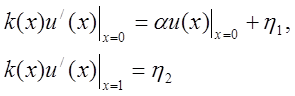

Тогда консервативная разностная схема, т.е. схема, для которой выполняются разностные аналоги физических законов сохранения, имеет вид:

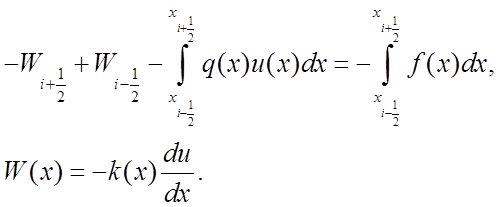
Получим  консервативную схему вида   где краевые условия учитываются следующим образом:

Проинтегрируем исходное уравнение теплопроводности на участке от 0 до h/2 и получим

                                    

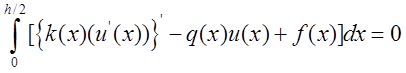
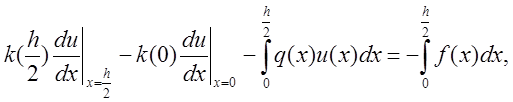
Приближая оставшиеся интегралы по формуле трапеций, и из вида третьих краевых условий   на левом конце 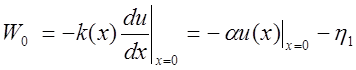  получаем выражение:

,

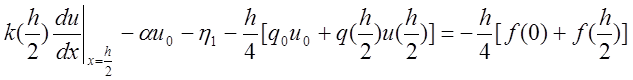Поскольку интеграл мы рассматривали от 0 до h/2, то для точки h/2 центральная разность будет иметь вид:

                                     ,

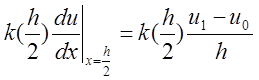Тогда уравнение примет вид:   

,

Группируя члены уравнения при , получим первое уравнение системы

.

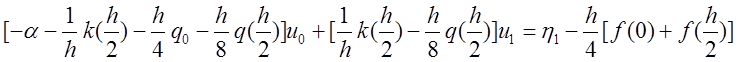Аналогично рассмотрим интеграл на участке от 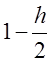 до 1 и получим:

                        ,

                     

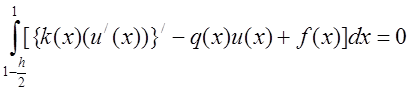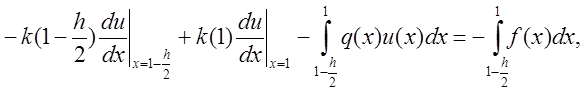
Приближая оставшиеся интегралы по формуле трапеций, и из вида вторых краевых условий   на правом конце 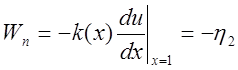    получаем выражение:

,

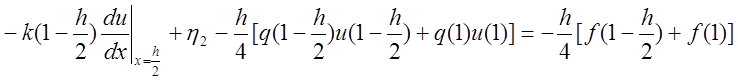Поскольку интеграл мы рассматривали от 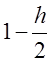 до 1, то для точки 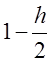центральная разность будет иметь вид:

                                     ,

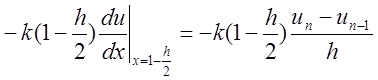Тогда уравнение примет вид:   

,

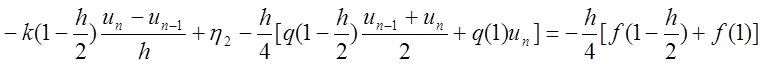Группируя члены уравнения при , получим последнее уравнение системы

.

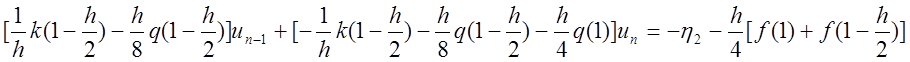Второе уравнение системы получаем:

,

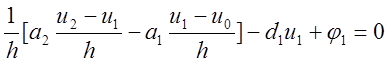Далее группируя члены при  получим:

,

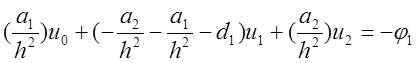Помножим все на h²:

.

В итоге получаем следующую систему уравнений с учетом

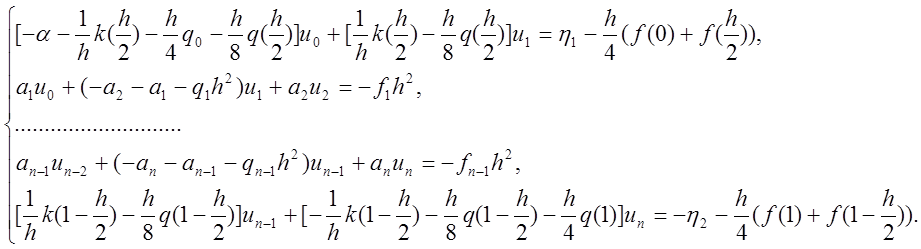
Отсюда получаем трехдиагональную матрицу вида

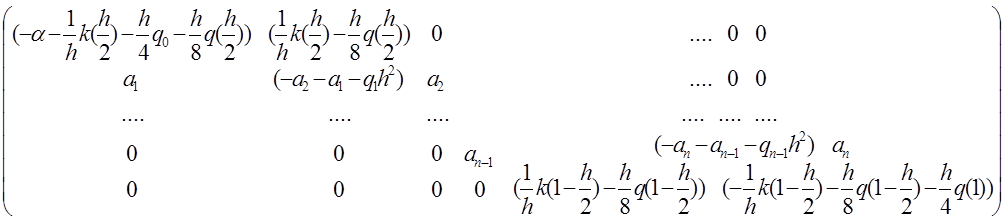
и вектор правой части:

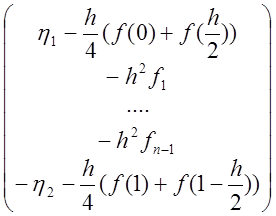
Для решения полученной СЛАУ будем использовать метод прогонки. Полученную матрицу будем хранить в диагональном формате.

4)Оценка порядка аппроксимации.

Дано уравнение:

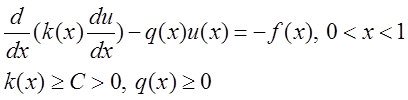
Выбираем трехточечный шаблон . Тогда разностная схема примет вид: , который можно переписать 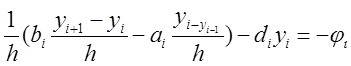 или иначе 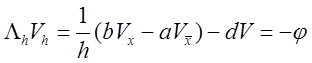. Теперь оценим погрешность аппроксимации:

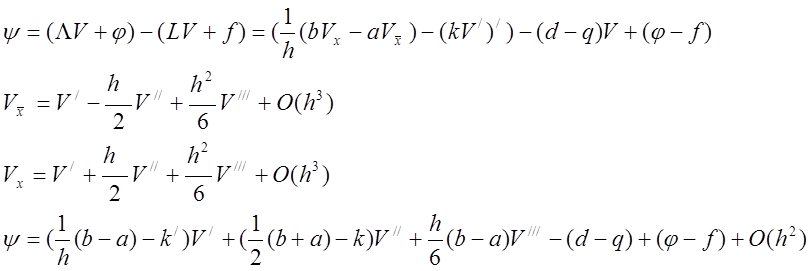
При выполнении следующих условий

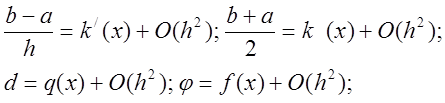
схема будет иметь второй порядок аппроксимации.

Тестовые задачи.

1.  Аналитическое решение уравнения (2.3): .

Краевые условия: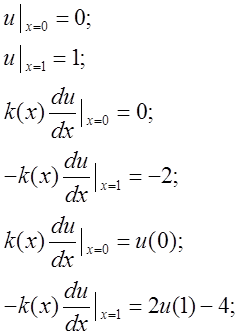

2. Аналитическое решение уравнения (2.3): . Краевые условия:

                                              

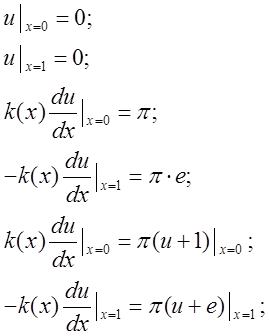
3. Аналитическое решение уравнения (2.3): . Краевые условия:

                                          

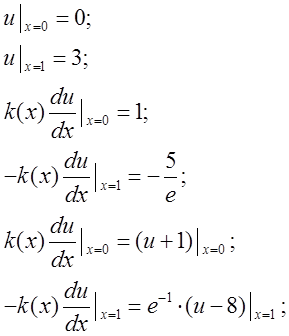
Первые краевые условия:

 Тест 1:

x		Y(h=0.1)	Y(h=h/2)	Y(h=h/4)	Y*
0		0	0	0	0
0.1		9.99999999999999e-003	9.99999999999996e-003	9.99999999999959e-003	1.00000000000000e-002
0.2		4.00000000000000e-002	3.99999999999999e-002	3.99999999999992e-002	4.00000000000000e-002
0.3		9.00000000000000e-002	8.99999999999999e-002	8.99999999999988e-002	9.00000000000000e-002
0.4		1.60000000000000e-001	1.60000000000000e-001	1.59999999999998e-001	1.60000000000000e-001
0.5		2.50000000000000e-001	2.50000000000000e-001	2.49999999999998e-001	2.50000000000000e-001
0.6		3.60000000000000e-001	3.60000000000000e-001	3.59999999999998e-001	3.60000000000000e-001
0.7		4.90000000000000e-001	4.90000000000000e-001	4.89999999999998e-001	4.90000000000000e-001
0.8		6.40000000000000e-001	6.40000000000000e-001	6.39999999999999e-001	6.40000000000000e-001
0.9		8.10000000000000e-001	8.10000000000000e-001	8.09999999999999e-001	8.10000000000000e-001
1		1	1	1	1

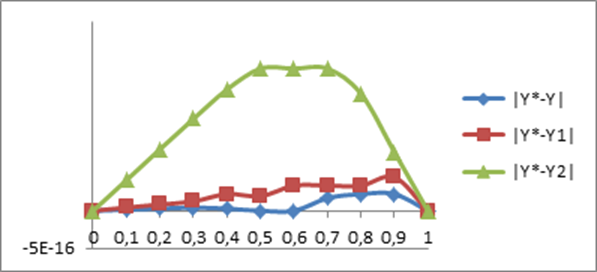
Тест 2: