Решение системы линейных неоднородных дифференциальных уравнений. Вариант № 1

2)  Это уравнение в полных дифференциалах:

 ;

3)  Это уравнение, не решённое относительно производной:

 ;

4)  Это уравнение, допускающее понижение порядка:

 ;

--------------------------------------------------------------------------------------------------------------------------------------------

II.  Решить систему линейных неоднородных дифференциальных

             уравнений вида :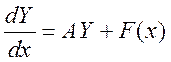

Задание:

1.  Методом вариации постоянных:

 ;     ;

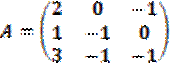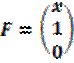2.  Методом Коши:

 ;       ; 

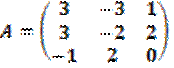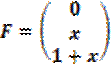Решение:

1)   Для начала решим однородную систему , решением которой имеет вид

.

Найдём собственные значения и векторы:

  ;

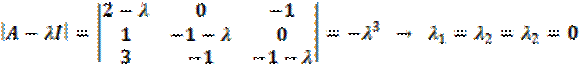Так как,  , имеем один собственный вектор:

 ;

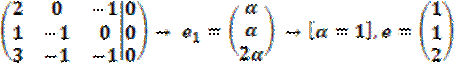Найдём присоединённый вектор первого порядка:

 ;

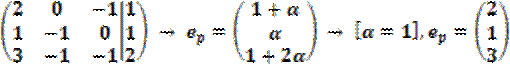Найдём присоединённый вектор второго порядка:

 ;

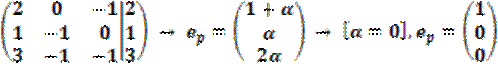Построим матрицу перехода и ЖНФ:

  ;                ;

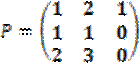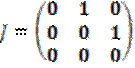Построим матричную экспоненту и  фундаментальную матрицу решений:

  ;     ;

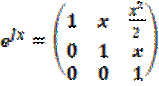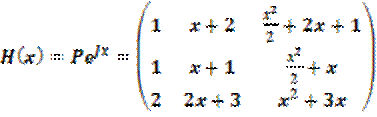Далее полагаем С не постоянным а переменным и находим вектор производных:

 ;

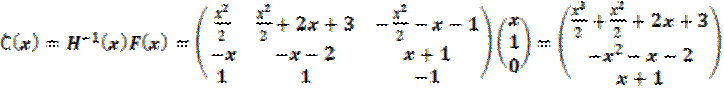Теперь осталось почленно проинтегрировать вектор производных и умножить результат на фундаментальную матрицу решений:

 ;

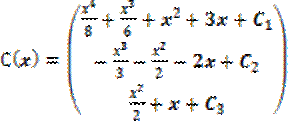Итак, ответ имеет вид:

 ;

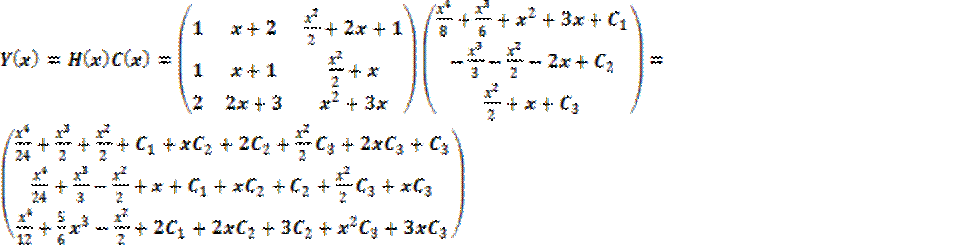2)  Найдём фундаментальную матрицу решений:

  ;

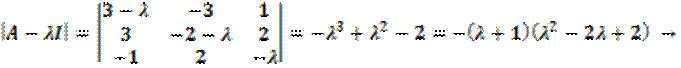
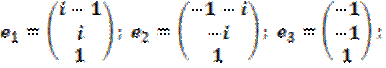
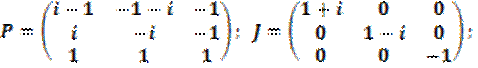
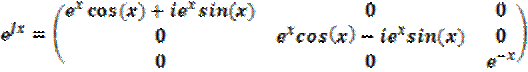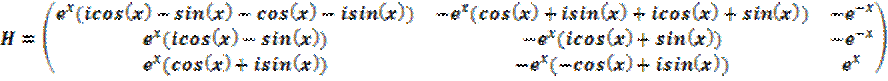
К первому столбцу прибавим второй и поделим на два, а из второго вычтем первый и поделим на (2i):

 ;

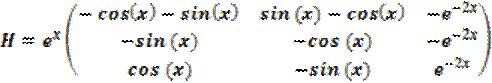Далее, найдём фундаментальную матрицу решений для сопряжённой системы:

  ;

  ;

   ;

 ;

  

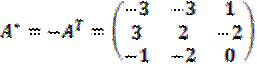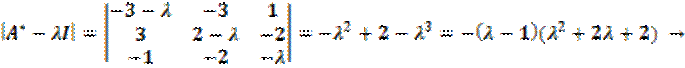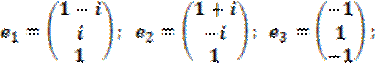
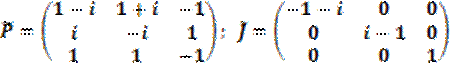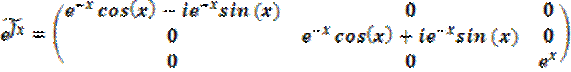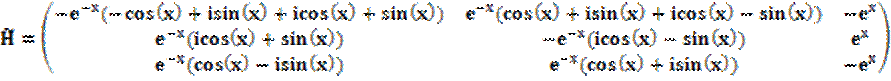
Заменим первый и второй столбцы их линейными комбинациями так, чтобы матрица стала вещественной:

;

  ;

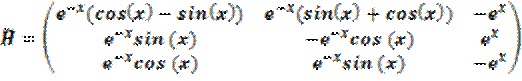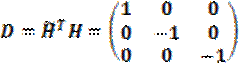Далее, найдём вектор производных:

  ;

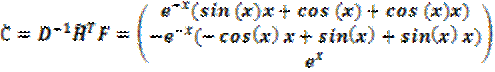Почленно интегрируем вектор производных:

  ;

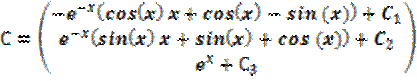Ответ:

  ;

------------------------------------------------------------------------------------------------------------------------------------------

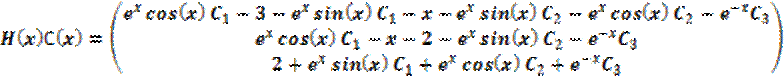III.  Решить неоднородное дифференциальное уравнение n-го порядка методом вариации постоянных:

Задание:

1.    ;

2.    ;

Решение:

1)  ;

Для начала, найдём решение соответствующего однородного уравнения. Для этого запишем характеристическое уравнение:

   ;

Составим общее решение соответствующего однородного уравнения:

  ;

Тогда решением соответствующего неоднородного уравнения будет:

  ;

Найдём неизвестную функцию из условия:

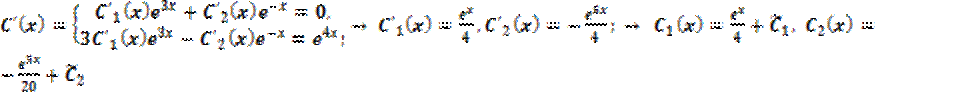
Итак, ответ можно записать в виде:

  ;

2)    ;

  ;

  ;

  ;

  ;

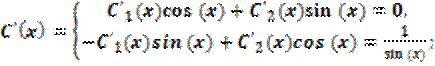
Ответ:   ;