Министерство образования и науки Российской Федерации.
Новосибирский государственный технический университет.
Кафедра прикладной математики.
Расчетно-графическое задание по дисциплине
Дифференциальные уравнения.
Выполнил: Шишкин И.П.
Группа: ПМ-53
Вариант: 17
Проверил: Баландин М.Ю.
Новосибирск
2007г.
I.
1. Определить тип и решить дифференциальные уравнения:
Данное уравнение является уравнением в полных дифференциалах.
1.
![]()
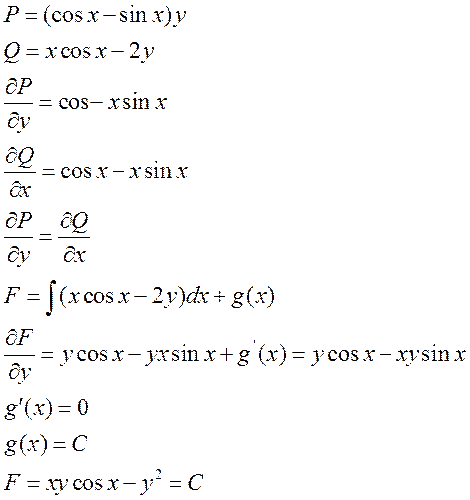
Ответ: ![]()
2. Определить тип и решить дифференциальные уравнения:
![]()
Дифференциальное уравнение третьего порядка, допускающее понижение степени.
Проверим уравнение на линейность:
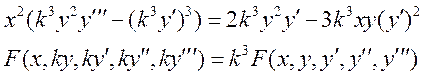 ,
,
Значит можно провести замену
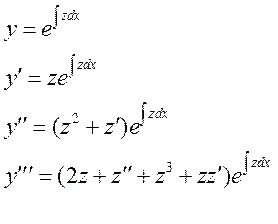
Получаем:
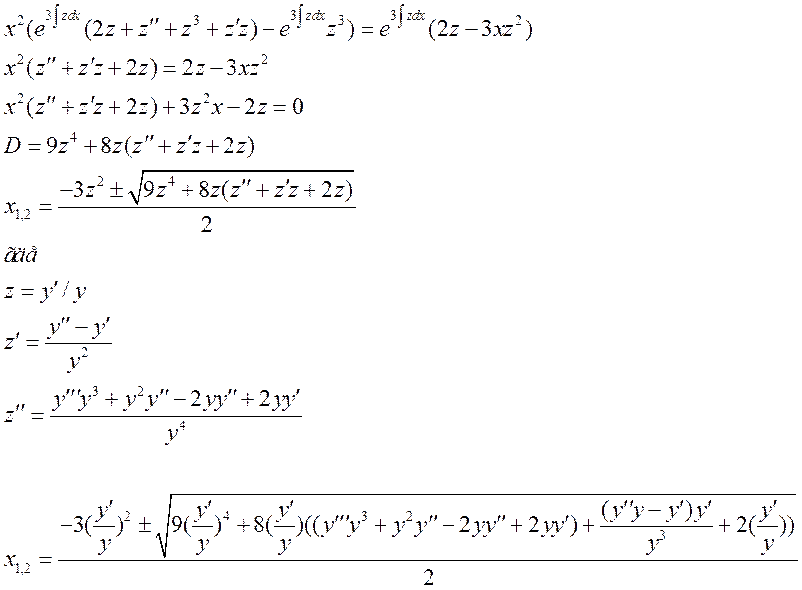
Ответ:
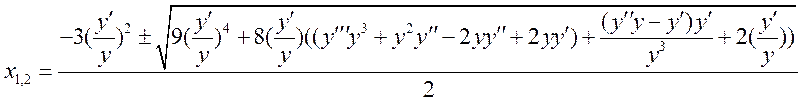
3. Определить тип и решить дифференциальные уравнения:
![]()
Данное уравнение является линейным уравнением первого порядка.
Решим
сначала ![]()
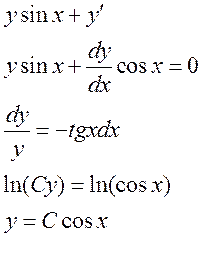
Заменим теперь произвольную постоянную С на функцию С(x)
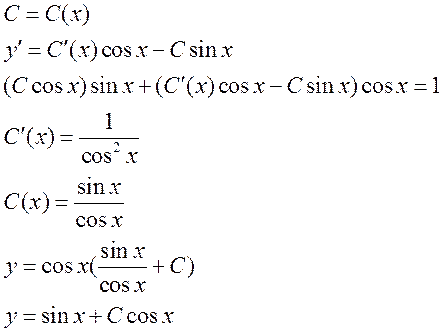
Ответ:
![]()
4. Определить тип и решить дифференциальные уравнения:
![]()
Данное
уравнение можно преобразовать к 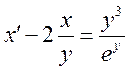 , которое является
линейным относительно x
, которое является
линейным относительно x
Решим
сначала 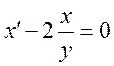
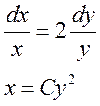
Заменим теперь произвольную постоянную С на функцию С(y)
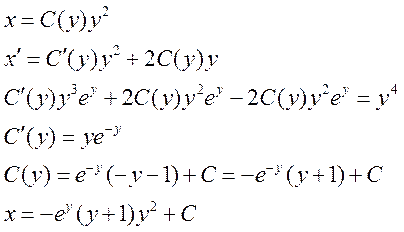
Ответ: ![]()
II.
1.Решить систему линейных
неоднородных дифференциальных уравнений вида 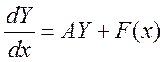 методом
вариации постоянных.
методом
вариации постоянных.
В условии в матрице А элемент А33 заменен с 10 на -10
Условие было изменено по согласованию с преподавателем.
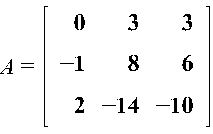
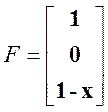
Найдем собственные значения матрицы А:
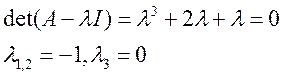
Далее найдем собственные вектора:
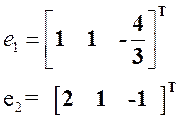 ,
,
Где
e1 соответствует
значению ![]() , е2
, е2 ![]()
Найдем присоединенный к e1 вектор:
![]()
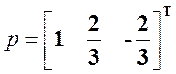
Составим из них матрицу перехода P:
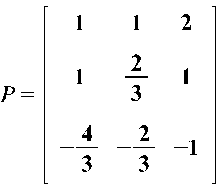
Соответствующая матрица J будет иметь вид:
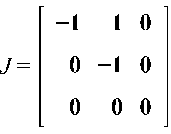
Найдем
матрицу ![]() :
:
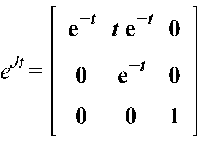
Далее
найдем матрицу ![]() :
:
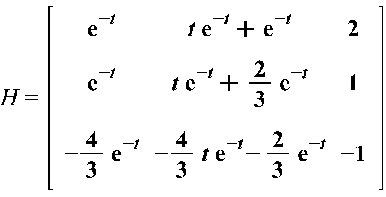
Умножим
матрицы ![]() получим:
получим:
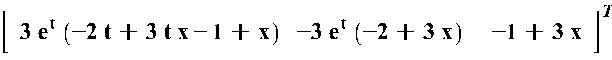
Далее
посчитав интегралы от каждого элемента вектора ![]() составим
из них соответствующий столбец:
составим
из них соответствующий столбец:
![]()
Получим ответ:
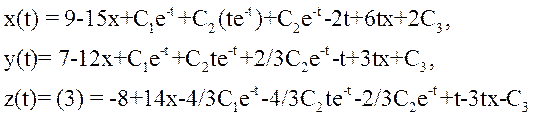
Ответ :
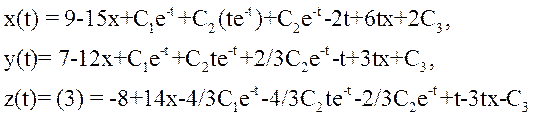
2. Решить систему линейных
неоднородных дифференциальных уравнений вида 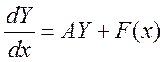 методом
Коши.
методом
Коши.
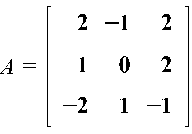
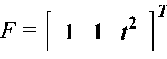
Найдем собственные значения матрицы А:
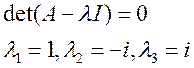
Далее найдем собственные вектора:
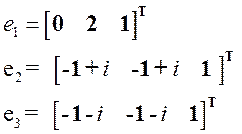 ,
,
Составим матрицу перехода Р:
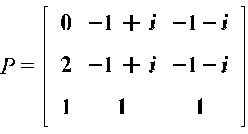
Соответствующая матрица J будет иметь вид:
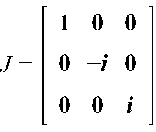
Найдем
матрицу ![]() :
:
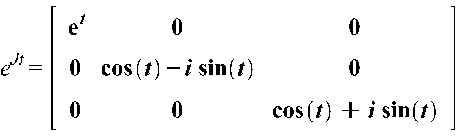
Далее
найдем матрицу ![]() :
:
H= 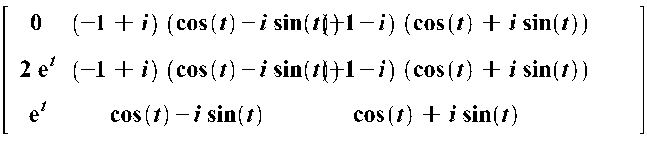
Найдем -A*. (В случае вещественных чисел A*=AT):
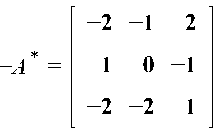
Собственные значения данной матрицы равны собственным значениям матрицы А, взятым с обратным знаком:
![]()
Собственные вектора будут выглядеть следующим образом:
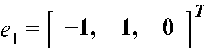
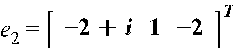

Составим матрицу перехода Р:
![]()
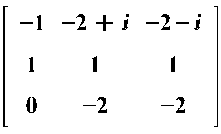
Соответствующая матрица J будет иметь вид:
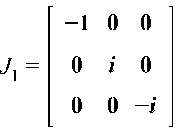
Найдем
матрицу ![]() :
:
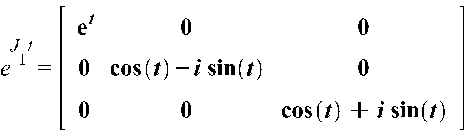
Далее
найдем матрицу ![]() :
:
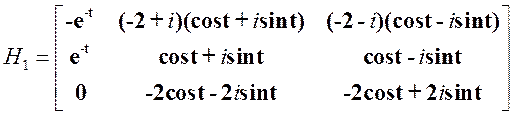
Умножим матрицы H и H1:
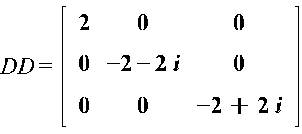
Умножим матрицы H1 иF:
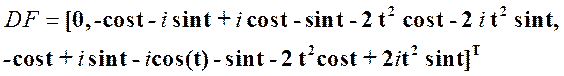
Далее, посчитав интегралы от каждой строки столбца H1F составим из них соответствующий столбец:
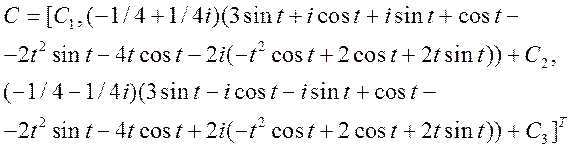
Умножив матрицы H1 и С получим:
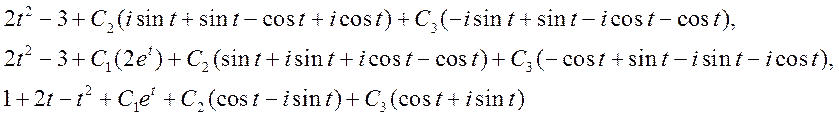
![]()
Ответ:
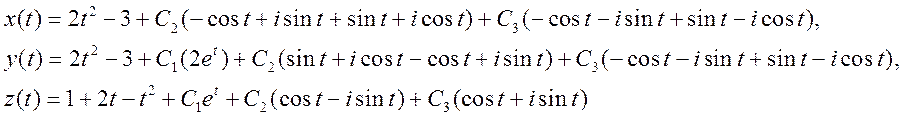
III. Решить неоднородное дифференциальное уравнение N-порядка методом вариации постоянных:
1.
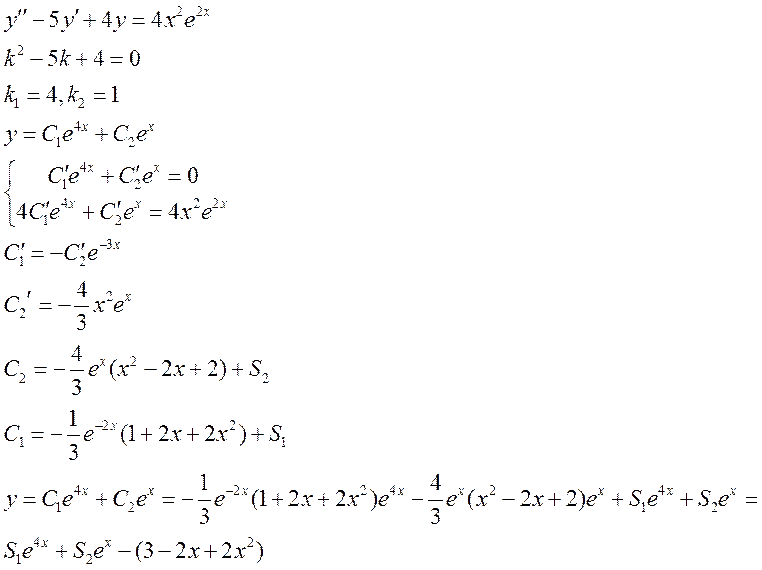
Ответ: ![]()
2. Решить неоднородное дифференциальное уравнение N-порядка методом вариации постоянных:
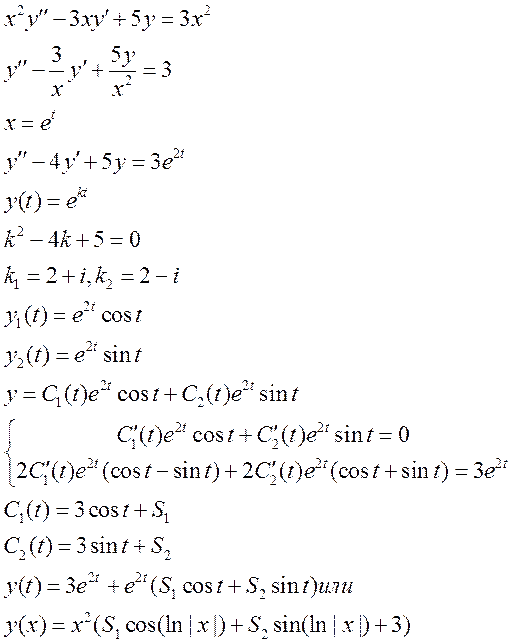
Ответ:
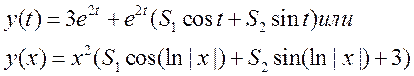
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.