Определение. Уравнения
![]() ,
(3)
,
(3)
называются
уравнениями, не разрешенными относительно производной. В уравнении (3) функция ![]() обычно считается параметром и обозначается
обычно считается параметром и обозначается
![]()
![]() . Так как функция
. Так как функция ![]() в общем случае нелинейна по параметру
в общем случае нелинейна по параметру ![]() , то уравнение (3) при определенных
условиях эквивалентно некоторому множеству (возможно, бесконечному) уравнений
вида
, то уравнение (3) при определенных
условиях эквивалентно некоторому множеству (возможно, бесконечному) уравнений
вида
![]() (4)
(4)
Достаточные условия приведения уравнения (3) к виду (4) сформулированы в теореме.
Теорема существования и единственности. Пусть в
некотором параллелепипеде с центром в точке ![]() функция
функция
![]() непрерывна по совокупности переменных
вместе с частными производными
непрерывна по совокупности переменных
вместе с частными производными 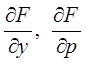 , причем
, причем
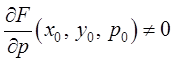 .
(5)
.
(5)
Тогда на некотором сегменте ![]() существует
единственное решение уравнения (3), удовлетворяющее начальному условию (2),
производная которого
существует
единственное решение уравнения (3), удовлетворяющее начальному условию (2),
производная которого ![]() .
.
Замечание. Тройка ![]() удовлетворяет
уравнению (3). Если уравнение (3) можно разрешить относительно параметра
удовлетворяет
уравнению (3). Если уравнение (3) можно разрешить относительно параметра ![]() , т. е. привести к виду (4), то его
решение ищется как для уравнения, разрешенного относительно производной. В
случае, когда уравнение (3) неприводимо к виду (4), можно воспользоваться
методом введения параметра. Рассмотрим
уравнение
, т. е. привести к виду (4), то его
решение ищется как для уравнения, разрешенного относительно производной. В
случае, когда уравнение (3) неприводимо к виду (4), можно воспользоваться
методом введения параметра. Рассмотрим
уравнение ![]() как уравнение поверхности в трехмерном пространстве
как уравнение поверхности в трехмерном пространстве ![]() .
.
Сделаем замену переменных: ![]() .
Тогда, так как
.
Тогда, так как ![]() , то
, то
 .
.
Выражая из последнего соотношения ![]() ,
получаем уравнение, разрешенное относительно производной. Особый интерес
представляют два частных случая уравнений, не разрешенных относительно производной
[2].
,
получаем уравнение, разрешенное относительно производной. Особый интерес
представляют два частных случая уравнений, не разрешенных относительно производной
[2].
1. Если исходное уравнение
можно разрешить относительно ![]() :
: ![]() , то считая, параметрами
, то считая, параметрами ![]() и
и ![]() ,
получаем
,
получаем ![]()
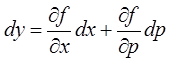 . Подставляя это
соотношение в исходное уравнение, получаем уравнение, разрешенное относительно
производной:
. Подставляя это
соотношение в исходное уравнение, получаем уравнение, разрешенное относительно
производной:  . Наиболее известные уравнения
такого типа – это уравнения Клеро и Лагранжа.
. Наиболее известные уравнения
такого типа – это уравнения Клеро и Лагранжа.
Уравнение Лагранжа: ![]() .
.
Уравнение Клеро: ![]() .
.
2. Если исходное уравнение
можно разрешить относительно ![]() :
: ![]() , то, выбрав в качестве параметров
, то, выбрав в качестве параметров ![]() и
и ![]() , получим
дифференциальное уравнение
, получим
дифференциальное уравнение 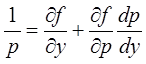 .
.
Определение. Множество точек в пространстве ![]() ,
в которых нарушается условие (5) теоремы существования и единственности, задается
уравнениями:
,
в которых нарушается условие (5) теоремы существования и единственности, задается
уравнениями:
![]() ,
,
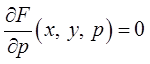 . (6)
. (6)
Кривая, определяемая условиями (6), называется дискриминантной кривой. Этой кривой принадлежат все особые точки уравнения (3). Кривая, описываемая уравнениями (6), – множество точек, определяющее особое решение уравнения (3).
Рассмотрим однородную линейную систему дифференциальных уравнений (ОСДУ)
 ,
(1)
,
(1)
где A – матрица с постоянными коэффициентами ![]() , Y – неизвестная вектор-функция
, Y – неизвестная вектор-функция ![]() . Общее
решение системы имеет вид
. Общее
решение системы имеет вид ![]()
![]() ,
где C – вектор произвольных постоянных [1].
,
где C – вектор произвольных постоянных [1].
Согласно теореме о приведении матрицы к квазидиагональному
виду [3] матрица A может
быть представлена следующим образом: ![]() , где J – жорданова форма матрицы A;
S – матрица, составленная из собственных и
присоединенных векторов матрицы A. Тогда систему
(1) можно записать как
, где J – жорданова форма матрицы A;
S – матрица, составленная из собственных и
присоединенных векторов матрицы A. Тогда систему
(1) можно записать как 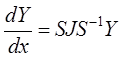 или
или 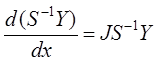 . Сделаем замену переменных
. Сделаем замену переменных ![]() и запишем ОСДУ покомпонентно для случая,
когда J – одна
жорданова клетка размерности
и запишем ОСДУ покомпонентно для случая,
когда J – одна
жорданова клетка размерности ![]() :
:
 ;
;
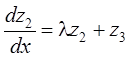 ;
;
.... ....
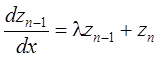 ;
;
 .
.
Решая эту систему, получим: ![]() ,
, ![]()
![]() , ...,
, ..., ![]() . Тогда общее решение ОЛСДУ:
. Тогда общее решение ОЛСДУ: ![]() .
.
Если все собственные значения матрицы A действительны и различны, то общее решение ОЛСДУ 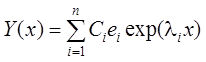 , где
, где ![]() –
произвольные постоянные;
–
произвольные постоянные; ![]() – собственные векторы
матрицы A;
– собственные векторы
матрицы A; ![]() – собственные
значения матрицы A.
– собственные
значения матрицы A.
Если матрица A вещественная,
и среди ее собственных значений есть комплексно-сопряженные, то частными
решениями ОЛСДУ будут не только решения ![]() , но и
решения вида
, но и
решения вида ![]() и
и ![]() [1].
[1].
Рассмотрим неоднородную линейную систему ДУ (НЛСДУ):
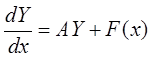 .
(2)
.
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.