Дифференциальные уравнения. Часть I: Методические указания к выполнению расчетно-графической работы, страница 5

Продолжение таблицы

Номер варианта	Матрица A, вектор правой части F
16
17
18
19
20
21
22
23

Окончание таблицы

2) методом Коши:

Продолжение таблицы

Номер варианта		Матрица A, вектор правой части F
6
7
	8
	9
	10
	11
	12
	13

Продолжение таблицы

Номер варианта			Матрица A, вектор правой части F
	14
	15
	16
	17
		18
		19
		20

Окончание таблицы

Номер варианта		Матрица A, вектор правой части F
	21
	22
	23
	24
	25

III. Решить неоднородное дифференциальное уравнение n-го порядка методом вариации постоянных:

1.  .

2.  .

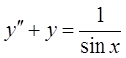3.  .

4.  .

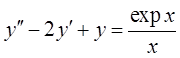5.  .

6.  .

7.  .

8.  .

9.  .

10.  .

11.  .

12.  .

13.  .

14.  .

15.  .

16.  .

17.  .

18.  .

19.  .

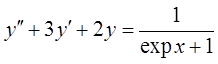20.  .

21.  .

22.  .

23.  .

24.  .

25.  .

Номер варианта	1	2	3	4	5	6
Номера задач	1,2	3,4	5,6	7,8	9,10	11,12
Номер варианта	7	8	9	10	11	12
Номера задач	13,14	15,16	17,18	19,20	21,22	23,24
Номер варианта	13	14	15	16	17	18
Номера задач	25,2	14,24	10,3	19,1	25,7	15,9
Номер варианта	19	20	21	22	23	24
Номера задач	18,4	22,6	21,8	20,5	17,7	16,12
Номер варианта	25
Номера задач	11,3

IV. Пример выполнения задания

I. Определить тип дифференциального уравнения и решить:

1) ;

2) ;

3) ;

4) ;

5) ;

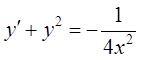6) определить область задания уравнения, область существования решения задачи Коши, область существования и единственности решения задачи Коши, особые решения.  .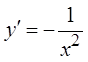

Решение

1. Уравнение  – это ДУ, приводящееся к уравнению с разделяющимися переменными заменой:  .

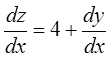Тогда . Получаем новое уравнение  – уравнение с разделяющимися переменными 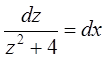. Общее решение ДУ:

 или , .

2. Уравнение  – уравнение Клеро. Перепишем ДУ в виде  продифференцируем по  и сделаем замену переменных: . Тогда получим ДУ