Математика \ Дифференциальные уравнения

Дифференциальные уравнения. Часть I: Методические указания к выполнению расчетно-графической работы, страница 3

Пусть , ( – частные решения ОЛСДУ) – фундаментальная система решений однородной системы (1). Будем искать решение неоднородной системы (2) в виде , где – неизвестная вектор-функция. Подставляя решение в систему (2), получаем соотношения для

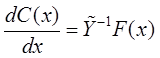; ; – вектор произвольных постоянных.

Тогда общее решение неоднородной системы ДУ имеет вид

Метод Коши

Рассмотрим однородную систему ДУ (1) и сопряженную к ней систему

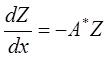. (3)

Пусть – нормальная фундаментальная система решений системы ДУ (1), – нормальная фундаментальная система решений системы ДУ (3). И для этих систем решений выполнены условия взаимной ортогональности: [1]. Это условие выполняется для всех . Будем искать решение неоднородной системы ДУ (2) в виде 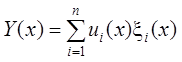, где – неизвестные функции. Подставляя решение в систему (2) и учитывая, то что – решения (1), получаем . Умножая последнее соотношение скалярно на , получаем уравнения для определения функций : .

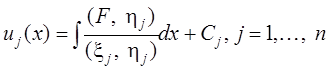Тогда общее решение НЛСДУ (2): .

III. Дифференциальные уравнения
n-го порядка

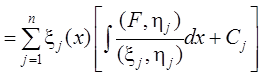Дифференциальные уравнения n-го порядка имеют вид

, (4)

если они не разрешены относительно старшей производной, и

, (5)

если они разрешены относительно старшей производной. Сделав замену переменных в уравнении (5): , получаем систему ДУ.

Простейшие случаи понижения порядка
дифференциального уравнения

1. Уравнение не содержит искомой функции и ее производных до порядка включительно: . Порядок уравнения можно понизить до заменой .

2. Уравнение не содержит независимого переменного x: . Порядок уравнения можно понизить на единицу заменой .

3. Левая часть уравнения (4) есть производная некоторого дифференциального выражения (n – 1)-го порядка.

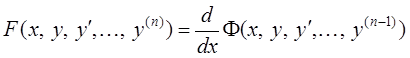Тогда первый интеграл этого уравнения: .

Иногда левую часть уравнения (4) привести к такому виду можно, домножив ее на некоторую функцию . Введение такого множителя приводит к появлению лишних решений, обращающих множитель в ноль [3]. Если множитель разрывен, то возможна потеря решения.

4. Уравнение (4) однородно относительно аргументов , т. е. для него выполняется тождество [2]. Тогда порядок уравнения (4) может быть понижен на единицу заменой: , где – новая неизвестная функция.

Линейные однородные
дифференциальные уравнения n-го порядка
с постоянными коэффициентами

Уравнения

, (6)

где – числа, называются линейными дифференциальными уравнениями с постоянными коэффициентами. Решение уравнения (6) будем искать в виде: . Подставляя решение в уравнение (6), получаем характеристическое уравнение

. (7)

1. Если корни уравнения (7) различны и действительны, то общее решение ДУ (6) можно представить в виде , где – произвольные постоянные; – корни уравнения (7); – частные решения ДУ (6).

2. Если коэффициенты уравнения (6) – действительные числа, а корни и – комплексно-сопряженные, то согласно теореме о действительном линейном операторе [1 – 3] решения , тоже будут частными решениями ДУ (6).

3. Если некоторый корень характеристического уравнения (7) имеет кратность , то частные решения, соответствующие этому корню, определяются следующим образом: .