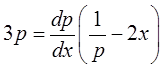 .
.
Перейдем от функции ![]() к обратной функции
к обратной функции ![]() [2]:
[2]:
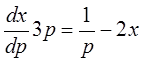 – это линейное ДУ первого порядка.
Перепишем его в виде
– это линейное ДУ первого порядка.
Перепишем его в виде
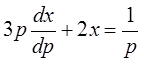
и решим методом вариации постоянной.
Общее
решение однородного ДУ 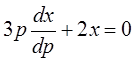 :
: 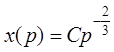 . Тогда решение неоднородного ДУ:
. Тогда решение неоднородного ДУ: 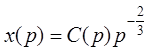 . Подставим решение в исходное уравнение и
получим соотношение для определения неизвестной функции
. Подставим решение в исходное уравнение и
получим соотношение для определения неизвестной функции ![]() :
:
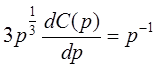 . Тогда
. Тогда 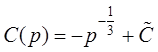 , а
, а 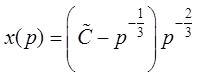 . Решение уравнения Клеро в параметрическом
виде
. Решение уравнения Клеро в параметрическом
виде 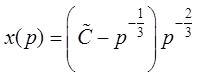 ,
, 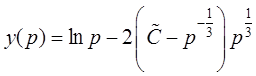 .
.
3. Уравнение ![]() – уравнение нелинейное относительно
– уравнение нелинейное относительно ![]() , перейдем к функции
, перейдем к функции ![]() :
: 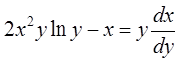 .
Перепишем ДУ в виде
.
Перепишем ДУ в виде 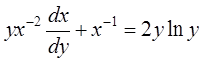 – это уравнение Бернулли. Замена
переменных
– это уравнение Бернулли. Замена
переменных 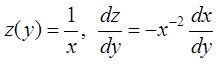 , тогда ДУ примет вид
, тогда ДУ примет вид 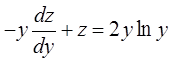 – неоднородное линейное дифференциальное
уравнение первого порядка. Решаем методом вариации постоянной. Решение
однородного ДУ
– неоднородное линейное дифференциальное
уравнение первого порядка. Решаем методом вариации постоянной. Решение
однородного ДУ 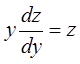 :
: ![]() . Тогда
решение неоднородного ДУ:
. Тогда
решение неоднородного ДУ: ![]() . Подставляя решение в
неоднородное ДУ, получаем
. Подставляя решение в
неоднородное ДУ, получаем 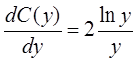 или
или ![]() . Общее решение неоднородного уравнения:
. Общее решение неоднородного уравнения: ![]() или
или ![]() .
.
4. Уравнение ![]() – ДУ второго порядка, допускающее
понижение порядка. Проверим выполнение условий однородности [3]: при замене
– ДУ второго порядка, допускающее
понижение порядка. Проверим выполнение условий однородности [3]: при замене ![]() уравнение примет вид
уравнение примет вид ![]() , где k –
постоянная величина. Уравнение однородно, значит, замена
, где k –
постоянная величина. Уравнение однородно, значит, замена ![]()
![]() понижает порядок
уравнения на единицу. Вычислим
понижает порядок
уравнения на единицу. Вычислим ![]() ,
, ![]()
![]() и подставим эти
выражения в исходное уравнение. После приведения подобных получаем ДУ
и подставим эти
выражения в исходное уравнение. После приведения подобных получаем ДУ ![]() . Общее решение этого уравнения
. Общее решение этого уравнения 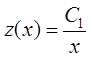 , тогда
, тогда 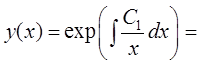
![]() .
.
5. Уравнение 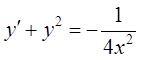 – это уравнение Риккати. Определим частное
решение в виде правой части:
– это уравнение Риккати. Определим частное
решение в виде правой части: 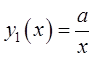 . Подстановка в ДУ
позволяет найти параметр
. Подстановка в ДУ
позволяет найти параметр ![]()
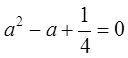 ,
т. е.
,
т. е. 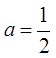 . Тогда частное решение:
. Тогда частное решение: 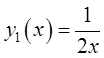 . Общее решение
. Общее решение ![]()
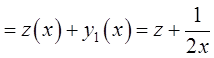 . Подставляя решение в уравнение Риккати, получаем
. Подставляя решение в уравнение Риккати, получаем
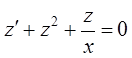 – это уравнение Бернулли. Используя прием
из пункта 3, решаем уравнение Бернулли. Общее решение:
– это уравнение Бернулли. Используя прием
из пункта 3, решаем уравнение Бернулли. Общее решение: 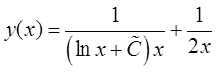 .
.
6. Правая часть уравнения 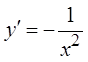 – функция, непрерывная для всех
– функция, непрерывная для всех ![]() . Общее решение ДУ:
. Общее решение ДУ: 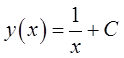 .
Интегральная кривая имеет горизонтальную асимптоту
.
Интегральная кривая имеет горизонтальную асимптоту ![]() .
Условие теоремы существования и единственности выполнено на всей действительной
прямой, кроме точки
.
Условие теоремы существования и единственности выполнено на всей действительной
прямой, кроме точки ![]() . Обратное уравнение:
. Обратное уравнение: 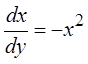 , общее решение:
, общее решение: 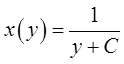 .
Прямая
.
Прямая ![]() – частное решение обратного уравнения.
– частное решение обратного уравнения.
II. Решить неоднородную систему дифференциальных
уравнений:
1) методом вариации постоянной
Пусть дана система ДУ 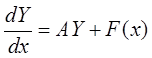 , где
, где 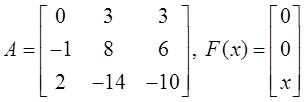 .
.
Собственные значения
матрицы A: ![]() .
Собственный вектор для
.
Собственный вектор для ![]() –
– ![]() ,
собственный и присоединенный векторы для
,
собственный и присоединенный векторы для ![]() :
: ![]() . Тогда матрица перехода
. Тогда матрица перехода 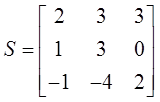 и жорданова форма матрицы A имеет вид
и жорданова форма матрицы A имеет вид 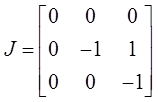 . Сделаем замену
. Сделаем замену ![]() в
однородной СЛДУ
в
однородной СЛДУ 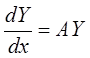 и получим систему линейных
дифференциальных уравнений:
и получим систему линейных
дифференциальных уравнений: 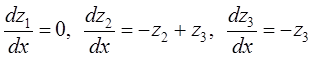 . Общее решение
однородной системы:
. Общее решение
однородной системы: ![]()
![]()
![]()
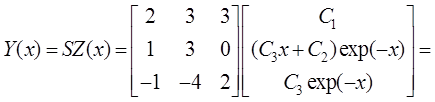
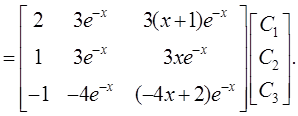
Фундаментальная
система решений 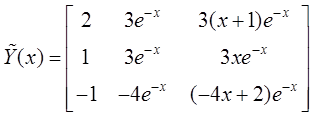 .
.
Тогда решение неоднородной
системы ДУ: ![]() ,
, ![]() .
.
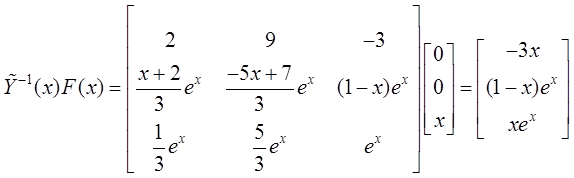 .
.
Тогда 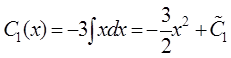 ,
, ![]()
![]() ,
, ![]() . Общее решение неоднородной
. Общее решение неоднородной
линейной системы
ДУ: 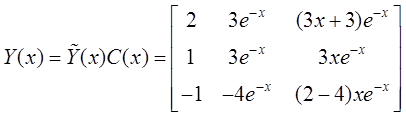
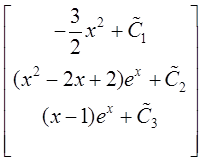 ;
;
2) методом Коши
Пусть дана система ДУ 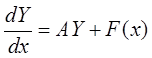 , где
, где 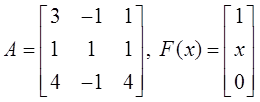 .
.
Собственные значения матрицы A:
![]() . Собственные векторы:
. Собственные векторы: ![]() ,
, ![]() ,
, ![]() . Нормальная система фундаментальных
решений соответствующей однородной задачи
. Нормальная система фундаментальных
решений соответствующей однородной задачи 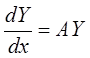 определяется
следующим образом:
определяется
следующим образом:
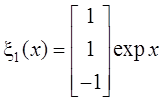 ,
, 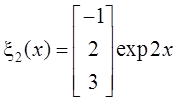 ,
, 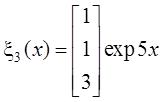 .
.
Нормальная фундаментальная система решений для сопряженной
задачи 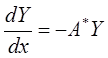 , где собственные значения и собственные
векторы матрицы
, где собственные значения и собственные
векторы матрицы ![]() имеют вид
имеют вид ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
состоит из вектор-функций
,
состоит из вектор-функций ![]()
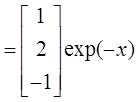 ,
,
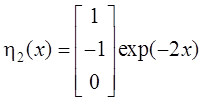 ,
, 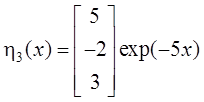 .
.
Проверим выполнение условий ортогональности: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Неизвестные функции
.
Неизвестные функции ![]() определяются выражением
определяются выражением 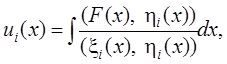
![]() . Тогда
. Тогда 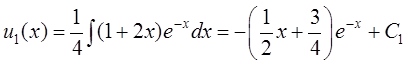 ,
,
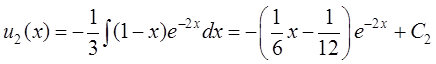 ,
, 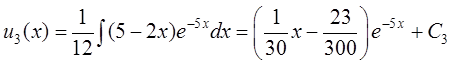 .
.
Общее решение неоднородной системы ДУ:
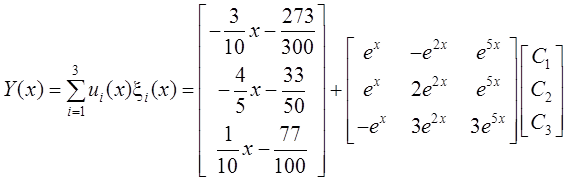 .
.
III. Решить линейное неоднородное дифференциальное уравнение n-го порядка методом вариации постоянной:
1) ![]() .
.
Решение однородного уравнения ![]() ищем в
виде
ищем в
виде ![]() . Характеристическое уравнение
. Характеристическое уравнение ![]() имеет корни
имеет корни ![]() . Тогда
общее решение однородного ДУ:
. Тогда
общее решение однородного ДУ: ![]()
![]() .
Решение неоднородного ДУ:
.
Решение неоднородного ДУ: ![]() . В соответствии с
идеей метода вариации постоянной [1] получаем условия для определения
неизвестных функций
. В соответствии с
идеей метода вариации постоянной [1] получаем условия для определения
неизвестных функций ![]() :
:
![]() . Решая
эту систему, определяем
. Решая
эту систему, определяем 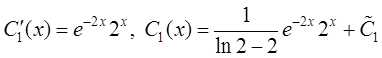 ,
, ![]()
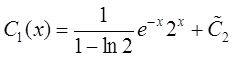 .
.
Общее решение неоднородного ДУ: 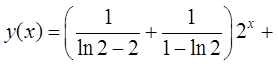
![]() ;
;
2) ![]() .
.
Это
уравнение Эйлера [3], сделаем замену ![]() , тогда ДУ примет вид
, тогда ДУ примет вид ![]() . Будем искать решение соответствующего
однородного уравнения в виде
. Будем искать решение соответствующего
однородного уравнения в виде ![]() . Характеристическое
уравнение:
. Характеристическое
уравнение: ![]() , его корни
, его корни ![]() .
Согласно теореме о действительном операторе [1] частные решения однородного ДУ
определяются соотношением
.
Согласно теореме о действительном операторе [1] частные решения однородного ДУ
определяются соотношением ![]() . Тогда общее решение
неоднородного ДУ:
. Тогда общее решение
неоднородного ДУ: ![]() . Аналогично пункту 3.1 получаем
условия для определения неизвестных функций
. Аналогично пункту 3.1 получаем
условия для определения неизвестных функций ![]()
![]()
![]() . Решение этой системы
. Решение этой системы ![]()
![]() . Общее решение
неоднородного ДУ:
. Общее решение
неоднородного ДУ: ![]()
![]() или
или ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.