Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 8

Достаточность. Пусть  - различные собственные значения оператора А. Собственные векторы, отвечающие собственному значению, образуют подпространство в L размерностью. Следовательно, линейный оператор А имеет  линейно независимых собственных векторов, соответствующих собственному значению. Т.о. мы имеем  собственных векторов. Покажем, что они линейно независимы в совокупности (от противного). Пусть это не так и равенство нулю линейной комбинации  возможно при ненулевых коэффициентах. Следовательно, пусть. Введем линейный оператор.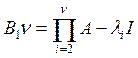

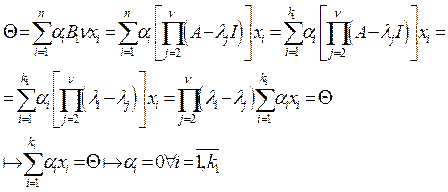
16. Достаточный признак оператора простой структуры. Доказать, что у всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство.

Теорема. Достаточный признак оператора простой структуры. Если все корни характеристического уравнения различны, то линейный оператор А имеет простую структуру.

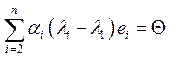Доказательство. Пусть. Покажем, что система  линейно независима: (1). Подействует линейным оператором:  (2). Подействует на (2) линейным оператором:  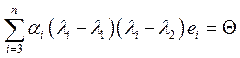 (3). Продолжая процесс вплоть до оператора  получим 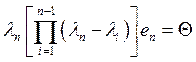 (4). Заметим, что (4) – это результат приложения оператора  к исходному уравнению. Из (4) следует. Если к исходному уравнению применить оператор  можно показать, что. И вообще соответствующим выбором оператора можно добиться, что все. Следовательно, - линейно независимы, а А – оператор простой структуры.

Теорема 1. У всякого линейного оператора в вещественном пространстве существует одномерное (двумерное) инвариантное подпространство.

Доказательство. Выберем в линейном пространстве Х базис. В этом базисе линейному оператору А соответствует матрица, преобразующая координаты  в координаты. Рассмотрим условие  в координатной форме:

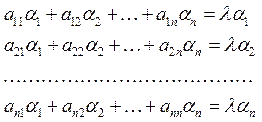(1)

Тогда ненулевое решение (1) существует, если  (2). И пусть  - корень уравнения (2). Возможны два случая:

1)  - вещественное, тогда существует  решение системы (1), определяющее координаты собственного вектора х. х порождает одномерное инвариантное пространство;

- комплексное (). Пусть  - это решение системы (1). Подставим эти числа в (1) и отделим вещественную часть от мнимой.
 (3).
Будем считать  - координатами некоторого вектора х, а  - координатами у, тогда  (4). Равенство (4) означает, что линейная оболочка  есть двумерное инвариантное подпространство относительное оператора.

17. Основные свойства симметричных операторов.

Определение. Самосопряженный оператор в евклидовом пространстве называется симметричным, если.

Утверждение. Пусть  - ортонормированный базис,. Пусть х и у в базисе е имеют координаты: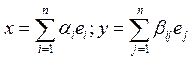. Тогда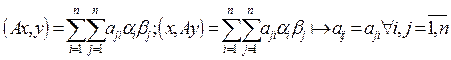. Это утверждение верно только в ортонормированном базисе.

Лемма 1. Для всякого симметричного оператора существует одномерное инвариантное пространство.

Доказательство. Из теоремы 1 (билет  16) следует, что нам нужно доказать существование вещественного корня  характеристического уравнения  (2). Предположим, что. Построим два вектор х и у такие, что.

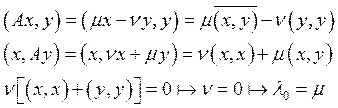
Лемма 2. Пусть А – симметричный оператор, а е – его собственный вектор, тогда множество векторов, ортогональных е, образуют (n-1)-мерное инвариантное пространство:.

Доказательство. Пусть.

Теорема 2. Существует ортонормированный базис, в котором матрица симметричного оператора А диагональна.

Доказательство. По лемме 1 линейный оператор А имеет хотя бы один собственный вектор, т.к. - инвариантное относительно линейного оператора А пространство, то в  существует собственный вектор … В итоге мы получим n собственных векторов, ортогональных по построению. Затем пронормируем их.

Теорема 3. Пусть  - квадратичная форма в n-мерном евклидовом пространстве, тогда существует ортонормированный базис, в котором эта квадратичная форма имеет вид: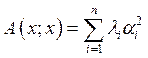, где  - собственные значения симметричного оператора.

Доказательство.. Выберем ортонормированный базис е из собственных векторов (существует по теореме 2).

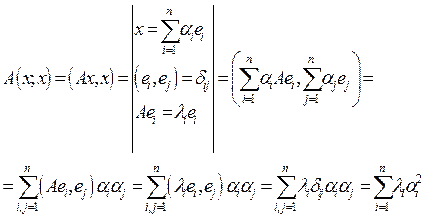
18. Ортогональные операторы и их свойства.

Определение. Линейный оператор, действующий в n-мерном евклидовом пространстве Х, называется ортогональным, если он сохраняет скалярное произведение.

Свойства.