Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 3

Определение. Суммой операторов А и В называется оператор С=А+В, если  (1).

Если.

Эта операция коммутативна и ассоциативна:

1)  ;

2)  .

В  существует нулевой элемент, который каждому  ставит в соответствие. Рассмотрим:

3)  ;

4) 

Введем операцию умножения оператора на число: (2). Покажем, что оператор С линейный.

Определение. Рассмотрим пространства Х, У и Z, заданные над одним и тем же полем F. Пусть  называется произведением оператора В на А:. Если  (3). Произведение линейных операторов также является линейным оператором:

.

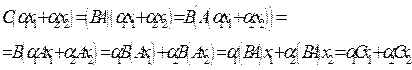Свойства:

5)  ;

6)  ;

7)  ;

8)  ;

9)  .

7.  Ядро и образ линейного оператора. Связь между дефектом, рангом и размерностью области определения линейного оператора. Обратный оператор. Невырожденный оператор.

Def: Оператор I Î W_XX называется тождественным (единичным) Оператором, если Ix=x; хÎХ.

Def: Оператор B Î W_XX называется обратным к А, если AB=BA=I (B=A^-1). Любой линейный оператор переводит θ->θ .

Def: R(A) ={y|y=Ax,xÎX}– образ А - подмножество  Y, замкнутое относительно операций -> подпространство.

Def: Ранг оператора rgA = dimR(A)

Def: Множество всех х, для которых Ах=θ называется ядром оператора А. N(A)={x|xÎХ, Ax=θ}. Ядро есть подпространство в Х.

Def: Размерность ядра называется дефектом n_A=dimN(A).

Рассмотрим соотношение между rgA и n_A линейного оператора. Пусть А:X->Y. Разложим линейное пространство Х в прямую сумму N(A) + M_A, где M­_A-любое дополнительное подпространство. Значит для  х Î Х справедливо единственное представление вида: x=x_n+x_m. x_n­ из ядра, x_m из доп. подпространства. Тогда y = Ax=A(x_n+x_m)=Ax­_n+Ax_m=Ax_m. То есть любой вектор из R(A) имеет хотя бы один прообраз из M_A. На самом деле он единственен. (Доказательство от противного (наличия у двух прообразов).

Таким образом мы установили взаимоднозначное соответствие между M_A  и R(A). Можно доказать, что оно является изоморфизмом.

dimX=dimN(A)+dimM_A=n_A-rgA

Def: Линейный оператор А:Х->X называется невырожденным, если его ядро состоит только из θ, в противном случае – оператор вырожденный.

8.  Определение и примеры нахождения матриц линейных операторов. Связь между координатами вектора – образа и вектора – прообраза. Изоморфизм пространства линейных операторов пространству прямоугольных матриц соответствующего размера.

Определение.

Пусть дан линейный оператор А:Х->Y, dimX=n. И некоторым базисом Х является e₁,...,e_n. dimY=m; g₁,...,g_m – базис Y. x=α₁e₁+...+α_ne_n . Ax= α₁Ae₁+...+α_nAe_n. Другими словами, лиейный оператор полностью определяется совокупностью образов Ae_i базисных векторов е. y Î L(Ae₁,...,Ae_n). Ae_j – вектор, содержащийся в Y и значит его можно разложить по базису Y.(*) Ae_j=a_1jg₁+...+a_njg_n. Коэффициенты a_ij определяют некоторую матрицу, в которой n строчек и n столбцов. Эту матрицу назовем матрицей А в базисах e₁,...,e_n g₁,...,g_n. Столбцами матрицы оператора служат координаты векторов Ае­₁,...,Ае_n в базисе g. Для того, чтобы определить элемент a_ij нужно найти образ Ae_j­­ и взять его i-ую координату.

Связь между координатами образа и прообраза.

Рассмотрим произвольный вектор х Î Х и его образ Ах.

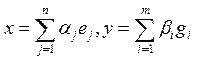 (1)..

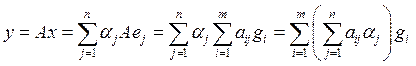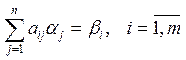
Тогда (2)y_g=A_gex_e

Таким образом, любой линейный оператор при фиксированных базисах пространств Х и Y порождает соотношение 2, связывающее координаты образа y_g b прообраза x_e.

---------По поводу изоморфизма в лекциях нет, но разбирали на практике-----------

9.  Связь между матрицами линейного оператора в разных базисах. Эквивалентные и подобные матрицы. Критерий эквивалентности двух матриц.

Пусть А:X->Y, dimX=n, dimY=m. e_i – I базис Х, f_i – II базис Х. g_i- I базис Y, h_i – II базис Y. P – матрица перехода от е к f, Q – матрица перехода от g к h. Возьмем произвольный х Î Х и разложим его по векторам обоих базисов. x=α₁e₁+...+α_ne_n=β₁f₁+...+β_mf_m=β₁(p₁₁e₁+...+p_n1e₁)+ ... +β_m(p_1me₁+...+p_nme₁)=e₁(p₁₁β₁+...+p_­1nβ_n)+...+e_n(p_n1β₁+...+p_nnβ_n).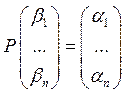. (3)x_e=Px_f. матрица Р невырождена, т.к. в противном случае имела бы место линейная зависимость между ее столбцами и следовательно между f₁...f_n. Пусть (4)y_g=A_gex_e, (5)y_n=A_hfx_f, A_ge и A_hf – матрицы оператора А в базисах е,g и f,h соответственно. То есть (6)y_g=Q_yh, где Q-матрица перехода g->h. y_h=Q^-1y_g; y_g=Q^-1A_ge­x_e=Q^-1A­_geP_xf=A_hfx_f. (7)=Q^-1A_geP. Если А: X->X. A_ff=P^-1A­_eeP