Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 12

Def: Множество точек, координаты которых удовлетворяют уравнению 1 называют  кривой второго порядка . Группу старших членов (2)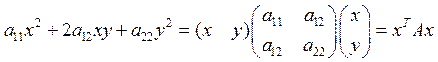 можно рассматривать как квадратичную форму от координат (х,у) вектора х. Поскольку матрица А-симметрична,  то  ортонормированный базис  из собственных векторов а, в котором матрица квадратичной формы диагональна и вещественна. Пусть матрица P=[p_ij] – матрица перехода от базиса е к базису. Тогда. Тогда (5)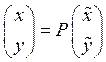. С учетом 5 запишем квадратичную форму 2. (6) Причем 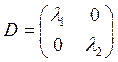(легко выводится умножением P^TAP). Следовательно в базисе квадратичная форма может быть записана в виде. Поскольку P^TP=I, матрица Р – ортогональная и геометрически переходу от базиса к базису соответствует поворот на некоторый угол φ против часовой стрелки.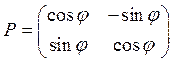. В силу справедливости 5,6 перепишем уравнение 1 в новых координатах. (10)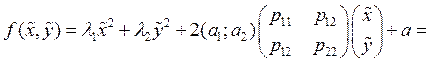 

Положим (11). Тогда λ₁λ₂ =detD=det(P^TAP)=detP^T detA detP=detA.

Значит           

Разделим случаи:

1)

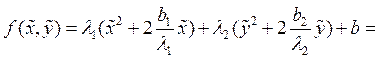
(13). Причем:, ,.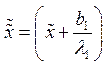

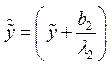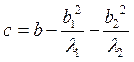А) Предположим, что, то есть все λ одного знака, тогда геометрическое место точек координаты которых удовлетворяют условию 13 представляет собой:

a.  Эллипс, если знак с противоположен знаку λ

b.  «Мнимый эллипс», если знак с=знаку λ

c.  точку, если с=0

В) Пусть, т.е. λ₁ и λ₂ разных знаков. Тогда 13 будет

a.   уравнением гиперболы: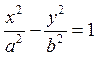, если c≠0

b.   И пары пересекающихся прямых, если c=0

24.  Приведение уравнения кривой второго порядка к каноническому виду с классификацией возможных типов в случае δ=0

3)  Пусть. Будем для определенности считать, что λ­₁=0, а λ₂≠0. Тогда уравнение 10 преобразуется к виду: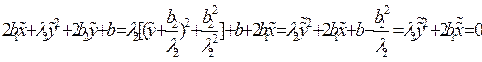. Полученное уравнение – уравнение параболы. Если же b₁=0, то уравнение приводится к следующему виду: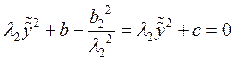. Это уравнение:

a.   пары параллельных прямых, если сλ₂<0

b.  совпадающих прямых, если с=0

c.  «мнимых параллельных прямых», если cλ₂>0

25.  Инварианты кривой второго порядка. Определение канонического уравнения кривой второго порядка по инвариантам.

Def: Инвариантой кривой называются функции коэффициентов уравнения кривой, которые не меняются при переходе от одной прямоугольной системы координат к другой.

Теорема. Для кривой второго порядка, , 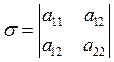 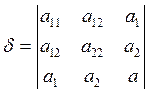являются инвариантами. В доказательстве рассматривается 2 случая: 1) параллельный перенос (производится замена переменных, открываются скобки, группируется ) 2) Поворот с использованием Р.(с помощью Р приводится к диагональной D=P^TAP, а затем вычисляются инварианты от D)

Кривая эллиптического типа		- Эллипс
		- Эллипс
		Точка
Кривая гиперболического типа		Гипербола
		Пара пересекающихся прямых
		Парабола
		Пара параллельных прямых

26.  Приведение уравнения поверхности второго порядка к каноническому виду с классификацией типов в случае, когда все λ_i отличны от нуля.

В случае, когда все λ_i отличны от нуля. Поверхность, путем преобразования квадратичной формы с помощью матрицы перехода Р (как в кривых только для матрицы 3х3) и затем преобразования координат и приведения их к каноническому виду, преобразуется в следующий вид:. Тогда имеем следующее.

С<0	 λi>0		Эллипсоид
	λ1>0 λ2>0 λ3<0		Однополостной гиперболоид
	λ1<0 λ2<0 λ3>0		Двуполостной гиперболоид
	 λi<0		Мнимый эллипсоид
С>0	 λi одного знака		Мнимый конус
	λ1>0 λ2>0 λ3<0		Конус

27.  Приведение уравнения поверхности второго порядка к каноническому виду с классификацией типов в случае, когда одно из λ_{i ­}равно нулю. 

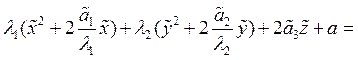
Пусть, для определенности, λ₃=0. Тогда уравнение поверхности примет вид:  (4). Если в 4, то  уравнение становится уравнением цилиндрической поверхности. (5). Снова будем считать, что с≤0, иначе умножим 5 на -1.