Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 14

Такой базис легко построить. Для этого достаточно выбрать какой-нибудь базис в R₁, дополнить его до базиса во всем пространстве и затем отбросить векторы исходного базиса из R₁. Число векторов в таком относительном базисе равно разности размерностей пространства и подпространства.  Всякую систему относительно линейно независимых векторов над R₁ можно дополнить до относительного базиса. Для этого нужно к выбранным векторам добавить какой-нибудь базис подпространства R₁. Получится некоторая система векторов из R, которые, как легко проверить, линейно независимы. Чтобы получить относительный базис, нужно дополнить эту систему до базиса во всем пространстве R, а затем отбросить базис подпространства.

Итак, пусть преобразование A в пространстве R имеет только одно собственное значение. Не ограничивая общности, можно предположить, что оно равно нулю. Рассмотрим цепочку подпространств:

0 Ì N₀⁽¹⁾ Ì … Ì N₀^(p) = N₀^(p+1) = …,

где подпространство N₀^(k) есть ядро преобразования A^k. Так как преобразование A в пространстве R не имеет отличных от нуля собственных значений, то, очевидно, N^(p) совпадает при этом со всем пространством R.

Выберем в максимальном из этих подпространств N₀^(p) базис относительно содержащегося в нем подпространства N₀^(p-1). Пусть векторы этого базиса будут: e₁,…, e_q

Очевидно, что это будут присоединенные векторы (p-1) – го порядка. т.к AN₀^(p) Ì N₀^(p-1), то векторы Ae₁,…,Ae_q лежат в N₀^(p-1). Покажем, что эти векторы линейно независимы в N₀^(p-1) относительно лежащего в нем подпространства N₀^(p-2). Действительно, пусть не все a_I = 0  и a₁Ae₁+…+a_qAe_q = A(a₁e₁+…+a_qe_q) Î N₀^(p-2)

Тогда вектор x = a₁e₁+…+a_qe_q Î N₀^(p-1) , а это противоречит предположению, что векторы e₁,…,e_q линейно независимы над N₀^(p-1).

Дополним векторы Ae₁,…,Ae_q до базиса в N₀^(p-1) относительно N₀^(p-2). Мы получим тогда q+s векторов Ae₁,…,Ae_q,f₁,…,f_s, которые представляют собой максимальное число линейно независимых присоединенных векторов порядка p-2

Снова применим к этим векторам преобразование A и полученную систему векторов из N₀^(p-2) дополним, как и выше, до базиса в N₀^(p-2) относительно N₀^(p-3).

Продолжая этот процесс, мы дойдем до подпространства N₀⁽¹⁾ и выберем базис в этом подпространстве, состоящий из максимального числа линейно независимых собственных векторов.

Расположим полученные векторы в следующую таблицу:

e₁    …   e_q

Ae₁ … Ae_q   f₁ … f_s

A²e₁ … A²e_q   Af₁ … Af_s

………………………….

………………………….

A^p-1e₁ … A^p-1e_q  A^p-2f₁ … A^p-2f_s … h₁ … h_r        (1)

Векторы нижней строчки образуют базис в подпространстве N₀⁽¹⁾

Векторы двух нижнех строчек образуют базис в N₀⁽²⁾, т.к. это и есть базис N₀⁽²⁾ относительно N₀⁽¹⁾ в соединении с базисом N₀^(1). Векторы трех нижних строчек образуют базис в N₀⁽³⁾ и т.д. Наконец все векторы таблицы образуют базис в N₀^(p), т.е. во всем пространстве R.

Покажем теперь, что в этом базисе матрица преобразования A имеет жорданову нормальную форму. Действительно, рассмотрим произвольный столбец таблицы (1), например, для определенности первый.

Обозначим для удобства A^p-1e₁ через, A^p-2e₁ – через  и т.д. и рассмотрим действие преобразования A  на каждый из этих векторов. Так как  - собственный вектор, отвечающий нулевому собственному значению, то A = 0

Дальше, по определению,

A = A A^p-2e₁  = A^p-1e₁ =

и аналогично A =

… A =

Таким образом, преобразование A переводит векторы первого столбца снова в себя, т.е. подпространство R₁, натянутое на эти векторы, инвариантно относительно A. Матрица преобразования A в подпространстве R₁ в базисе,…,  имеет вид

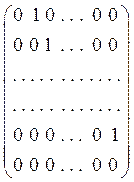(2) т.е это есть жорданова клетка, отвечающая собственному значению λ=0.

Аналогичное инвариантное подпространство отвечает каждому из столбцов таблицы (1), и размерность каждого такого подпространства равна числу векторов в соответствующем столбце. Так как матрица преобразования A в базисе, состоящем из векторов какого-либо столбца таблицы (1), имеет вид (2), то матрица преобразования во всем пространстве R в базисе, состоящем из всех векторов таблицы (1), состоит из жордановых клеток, число которых равно числу столбцов в этой таблице, а размер каждой клетки равен числу векторов соответствующего столбца.