Математика \ Геометрия и алгебра

Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 13

с<0	λ1>0 λ2>0	Эллиптический цилиндр
	λ1>0 λ2<0	Гиперболический цилиндр
	λ1<0 λ2<0	Мнимый эллиптический цилиндр
с>0	λi одного знака	Две мнимые пересекающиеся плоскости	Прямая х=0, y=0
с>0	λi разных знаков	Две мнимые пересекающиеся плоскости	Прямая х=0, y=0
c<0	Если λi одного знака	Эллиптический параболоид
	Если разных знаков	Гиперболический параболоид

28. Приведение уравнения поверхности второго порядка к каноническому виду с классификацией типов в случае, когда два из λ_i равны нулю.

Пусть, тогда уравнение поверхности примет вид: (7). Это пара параллельных плоскостей, различных, когда λ₁C<0, совпадающих, когда C=0, мнимых, если λ₁C>0.

Если a₂≠ 0 или a₃≠0, делаем замену, полагая: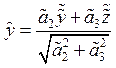,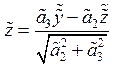. Подставляя в 7 получаем: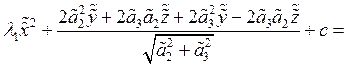 , где. Это кривая второго порядка на плоскости или параболический цилиндр.

29. Доказать теорему о возможности расщепления пространства X, в котором действует линейный оператор, в прямую сумму корневых подпространств: X = ⁽^p¹⁾₊⁽^p²⁾_{+ … +}⁽^pk⁾

Теорема 1: Пространство R можно разложить в прямую сумму инвариантных подпространств N₀⁽^p⁾ и M⁽^p⁾. При этом подпространство N₀⁽^p⁾ состоит только их собственных и присоединенных векторов, отвечающих собственному значению λ=0, а в подпространстве M⁽^p⁾ преобразование обратимо (т.е. λ=0 не является собственным значением преобразования A в подпространстве M⁽^p⁾.

Доказательство: для доказательства первого утверждения нам достаточно показать, что пересечение подпространств N₀⁽^p⁾ и M₀⁽^p⁾ равно нулю. Допустим противное, т.е пусть существует вектор y≠0 такой, что yÎM⁽^p⁾ и yÎN₀⁽^p⁾. Так как yÎM⁽^p⁾, то y=A^px.

Далее, так как yÎN₀⁽^p⁾, то A^py=0

Но из равенств (8) и (9) следует, что существует такой вектор x, для которого A^px≠0 и в то же время A²^px = A^py = 0

Это значит, что x есть присоединенный вектор преобразования A с собственным значением λ=0, не принадлежащий подпространству N₀⁽^p⁾, что невозможно, так как N₀⁽^p⁾ состоит из всех таких векторов.

Таким образом мы доказали, что пересечение N₀⁽^p⁾ и M₀⁽^p⁾ равно нулю. Так как сумма размерностей этих подпространств равна n (это ядро и образ преобразования A^p), то отсюда следует, что пространство R раскладывается в прямую сумму этих подпространств:

R = M⁽^p⁾N₀⁽^p⁾

Докажем теперь второе утверждение теоремы, т.е. что в подпространстве M⁽^p⁾ преобразование A не имеет нулевого собственного значения. Действительно, если бы это было не так, то в M⁽^p⁾ существовал бы вектор x≠0 такой, что A^px=0

Но это равенство означает, что xÎN₀⁽^p⁾, т.е. является общим вектором M⁽^p⁾ и N₀⁽^p⁾, а мы доказали, что таким вектором может быть только нуль.

Теорема 2: Пусть преобразование A пространства R имеет k различных собственных значений λ₁,….,λ_k. Тогда R можно разложить в прямую сумму k инвариантных подпространств N_λ₁⁽^p¹⁾,….,N_λk⁽^pk⁾:

R = N_λ₁⁽^p¹⁾ …. N_λk⁽^pk⁾

Каждое из подпространств N_λi⁽^pi⁾ состоит только из собственных и присоединенных векторов, отвечающих собственному значению λ_i

Другими словами, для каждого i существует такое число p_i, что для всех xÎN_λ_i⁽^pi⁾ :

(A-λ_iI) ^pi x = 0

30. Выбор базиса в корневом подпространстве. Расщепление корневого подпространства на прямую сумму циклических подпространств.

Определение. Векторы из пространства X называются относительно линейно независимыми над подпространством R₁, если никакая их линейная комбинация, отличная от нуля не принадлежит R₁

Определение. Базисом пространства R относительно пространства R₁ называется такая система e₁, … ,e_k линейно независимых векторов из R, которая после пополнения каким-нибудь базисом из R₁ образует базис во всем пространстве

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Скачать файл