Определение. Пусть даны квадратичная матрица А размерностью ![]() и функция
и функция ![]() скалярного
аргумента
скалярного
аргумента![]() . Распространим
. Распространим ![]() на матричное
значение аргумента. Если
на матричное
значение аргумента. Если![]() , то функция от
матрицы приобретает вид
, то функция от
матрицы приобретает вид![]() .
.
Теорема
Гамильтона. Пусть 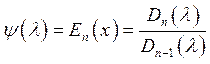 - минимальный многочлен. Разложим его на
множители
- минимальный многочлен. Разложим его на
множители ![]() (1), где
(1), где ![]() -
все различные собственные значения матрицы А. Степень же
-
все различные собственные значения матрицы А. Степень же ![]()
![]() чисел
чисел ![]() (2) будем называть значениями
функции
(2) будем называть значениями
функции ![]() на спектре матрицы А. Очевидно, чтобы
значения функции
на спектре матрицы А. Очевидно, чтобы
значения функции ![]() на спектре матрицы А полностью
определяют
на спектре матрицы А полностью
определяют![]() , т.е. все функции
, т.е. все функции![]() ,
имеющие одни и те же значения на спектре матрицы А имели одно и то же матричное
значение
,
имеющие одни и те же значения на спектре матрицы А имели одно и то же матричное
значение![]() . Т.о. для определения
. Т.о. для определения ![]() в общем случае достаточно найти многочлен
в общем случае достаточно найти многочлен![]() , который принимал бы те же значения на
спектре матрицы А, что и
, который принимал бы те же значения на
спектре матрицы А, что и![]() , и положить, что
, и положить, что![]() .
.
Определение. Если функция ![]() определена
на спектре матрицы А, то
определена
на спектре матрицы А, то![]() , где
, где ![]() - любой многочлен, принимающий на спектре
те же значения, что и
- любой многочлен, принимающий на спектре
те же значения, что и![]() , т.е.
, т.е.![]() .Среди
всех многочленов с комплексными коэффициентами, принимающих те же значения на
спектре, что и
.Среди
всех многочленов с комплексными коэффициентами, принимающих те же значения на
спектре, что и![]() , существует единственный
многочлен
, существует единственный
многочлен![]() , степень которого меньше m. Этот
многочлен однозначно определяется интерполирующими условиями:
, степень которого меньше m. Этот
многочлен однозначно определяется интерполирующими условиями:
 (3)
– интерполяционный многочлен Лагранжа-Сильвестра.
(3)
– интерполяционный многочлен Лагранжа-Сильвестра.
Определение. Пусть функция![]() , определена на спектре матрицы А, а
, определена на спектре матрицы А, а ![]() - соответствующий интерполяционный
многочлен. Тогда
- соответствующий интерполяционный
многочлен. Тогда![]() .
.
Замечание. Получили, что если ![]() матрицы
А не имеет кратных корней (матрица простой структуры) и в равенстве (1)
матрицы
А не имеет кратных корней (матрица простой структуры) и в равенстве (1)![]() , то для того, чтобы
, то для того, чтобы ![]() имело смысл достаточно, чтобы
имело смысл достаточно, чтобы ![]() была определена в точках
была определена в точках![]() , если же все
, если же все ![]() имеют
кратные корни, то в некоторых точках соотношения (2) должны быть
определены и производные до известного порядка.
имеют
кратные корни, то в некоторых точках соотношения (2) должны быть
определены и производные до известного порядка.
Свойства функций от матриц:
1)
Если ![]() -
собственные числа матрицы А n-ого порядка, то
-
собственные числа матрицы А n-ого порядка, то ![]() -
собственные числа матрицы
-
собственные числа матрицы![]() .
.
2)
Если матрицы А и В подобны, т.е.![]() , то матрицы
, то матрицы ![]() и
и ![]() также подобны, причем
также подобны, причем![]() .
.
Доказательство. Пусть![]() . Покажем, что
. Покажем, что![]() , используя метод математической индукции.
Для k=1, это очевидно. Пусть это верно и для k=m.
Докажем, что это верно и для
, используя метод математической индукции.
Для k=1, это очевидно. Пусть это верно и для k=m.
Докажем, что это верно и для
3)
k=m+1.
Действительно,![]() . Тогда
. Тогда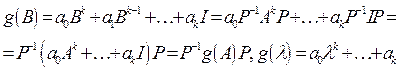 .
.![]() .
.
Т.о. две подобные матрицы имеют одинаковые минимальные многочлены и аналогично ![]() принимает одни и те же значение как на
спектре матрицы А так и на спектре матрицы В. Поэтому существует интерполяционный
многочлен
принимает одни и те же значение как на
спектре матрицы А так и на спектре матрицы В. Поэтому существует интерполяционный
многочлен![]() .
.
4)
Пусть А – квазидиагональная матрица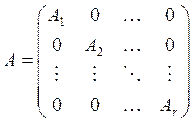 , тогда
, тогда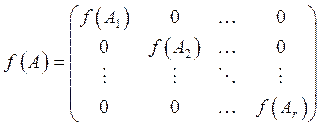 .
.
Доказательство. Обозначим через ![]() интерполяционный
многочлен функции
интерполяционный
многочлен функции ![]() на спектре матрицы А.
на спектре матрицы А. 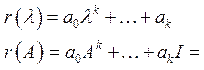
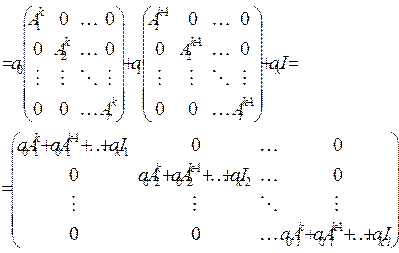 (5)
(5) .
Минимальный многочлен
.
Минимальный многочлен ![]() является аннулирующим
многочленом для матрицы
является аннулирующим
многочленом для матрицы![]() , поэтому из равенства
, поэтому из равенства![]() . Поэтому
. Поэтому ![]() и
и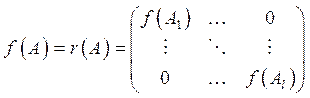 .
.
Интерполяционный
многочлен Лагранжа-Сильвестра. Пусть ![]() - минимальный многочлен матрицы А,
- минимальный многочлен матрицы А,![]() .
. 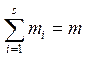 -
степень
-
степень![]() . Представим
. Представим 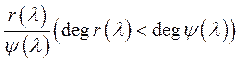 является
правильной дробью в виде суммы дробей:
является
правильной дробью в виде суммы дробей:  (6),
где
(6),
где ![]() - некоторые числа. Для определения
числителя простой дроби умножим обе части (6) на
- некоторые числа. Для определения
числителя простой дроби умножим обе части (6) на 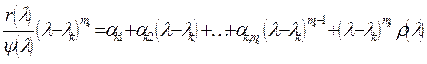 (7),
где
(7),
где ![]() - рациональная функция, не обращающаяся в
бесконечность при
- рациональная функция, не обращающаяся в
бесконечность при![]() . Обозначим через
. Обозначим через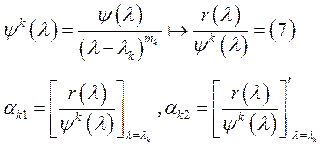 .
. 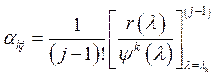 (8)
(8)
Формулы
(8) показывают, что числители ![]() в правой части (6)
выражаются через значения многочлена
в правой части (6)
выражаются через значения многочлена ![]() на спектре матрицы А, а
эти значения нам известны. А именно, они равны соответственным значения функции
на спектре матрицы А, а
эти значения нам известны. А именно, они равны соответственным значения функции
![]() и ее производной:
и ее производной: 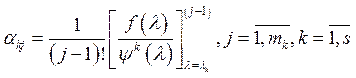 (9’).
После того, как все
(9’).
После того, как все![]() найдены, мы определим
найдены, мы определим ![]() по следующей формуле, которая получается
умножением обеих частей равенства (6) на
по следующей формуле, которая получается
умножением обеих частей равенства (6) на![]() :
: 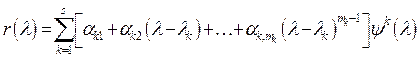 (10). Заметим, что в соотношении (10)
выражение в квадратных скобках в силу (9’) равно сумме первых
(10). Заметим, что в соотношении (10)
выражение в квадратных скобках в силу (9’) равно сумме первых ![]() членов разложения Тейлора по степеням
членов разложения Тейлора по степеням ![]() для
для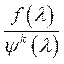 .
.
Основная
формула. Вернемся к (10).
Подставив в нее (9’) для коэффициентов ![]() и
объединив члены, содержащие одно и тоже значение
и
объединив члены, содержащие одно и тоже значение ![]() и
какой-либо ее производной, представим
и
какой-либо ее производной, представим ![]() в виде
в виде 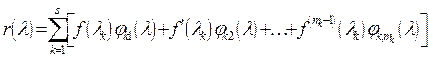 (11), где
(11), где ![]() -
полином
-
полином ![]() степени меньшей степени
степени меньшей степени![]() . Эти полиномы определяются заданием
. Эти полиномы определяются заданием ![]() и не зависит от выбора функции
и не зависит от выбора функции![]() . Число этих полиномов равно числу значений
. Число этих полиномов равно числу значений
![]() на спектре матрицы А и равно m, где m –
степень минимального многочлена. Из формулы (10) следует основная
формула для нахождения функции от матрицы, а именно:
на спектре матрицы А и равно m, где m –
степень минимального многочлена. Из формулы (10) следует основная
формула для нахождения функции от матрицы, а именно: 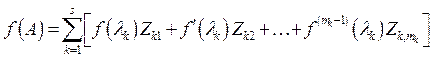 (12),
матрицы
(12),
матрицы ![]() являются компонентами матрицы А. Они
вполне определяются заданием матрицы А и не зависят от выбора функции
являются компонентами матрицы А. Они
вполне определяются заданием матрицы А и не зависят от выбора функции![]() . В правой части формулы (12),
функция
. В правой части формулы (12),
функция ![]() представлена только своими значениями на
спектре матрицы А.
представлена только своими значениями на
спектре матрицы А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.