Определение.
Будем называть m-плоскость, определяемую точками ![]() - m-плоскостью
- m-плоскостью![]() .
.
Определение. Если m=n-1, то такая плоскость называется гиперплоскостью или просто плоскостью.
Если мы умножим обе части уравнения (1) на
вектор u, перпендикулярный всем![]() , то
т.к.
, то
т.к.![]() , мы получим уравнение (4):
, мы получим уравнение (4):![]() , или
, или![]() , или
, или![]() .
.
Определение.
Вектор u ортогональный ко всем направляющим векторам ![]() и, следовательно, ко всем векторам,
направленным по плоскости, называется вектором нормали.
и, следовательно, ко всем векторам,
направленным по плоскости, называется вектором нормали.
Пусть ![]() - ортонормированный
базис в n-мерном аффинном пространстве, тогда х можно разложить
по этому базису:
- ортонормированный
базис в n-мерном аффинном пространстве, тогда х можно разложить
по этому базису: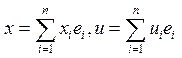 . Тогда (4) можно
записать, как
. Тогда (4) можно
записать, как 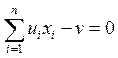 (5).
(5).
Уравнение плоскости по точке и вектору нормали. Если задана точка ![]() и
вектор нормали u, то т.к.
и
вектор нормали u, то т.к. ![]() удовлетворяет уравнению (4),
мы получаем, что
удовлетворяет уравнению (4),
мы получаем, что![]() .
.
Уравнение плоскости по точке и направляющим векторам. Если задана точка ![]() и ее
направляющие векторы
и ее
направляющие векторы![]() , то уравнение плоскости будет:
, то уравнение плоскости будет: 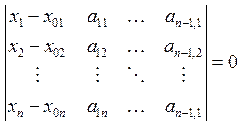 (8).
(8).
Уравнение плоскости по n точкам. Пусть даны n точек![]() , при
этом
, при
этом ![]() линейно независимы. Тогда уравнение
плоскости будет иметь вид:
линейно независимы. Тогда уравнение
плоскости будет иметь вид: 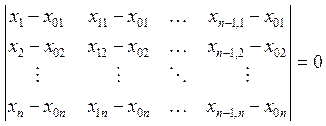 (9).
(9).
Теорема. Если
заданы n+1 точек![]() , то необходимым и
достаточным условие того, что точки
, то необходимым и
достаточным условие того, что точки ![]() лежат на одной
плоскости является линейная зависимость векторов
лежат на одной
плоскости является линейная зависимость векторов![]() .
.
Доказательство.
Необходимость.
Если точки ![]() лежат на одной плоскости, то n
векторов
лежат на одной плоскости, то n
векторов![]() , являющиеся линейными комбинациями n-1 направляющего
вектора
, являющиеся линейными комбинациями n-1 направляющего
вектора![]() , линейно зависимы.
, линейно зависимы.
Достаточность.
Если эти векторы линейно зависимы, то существует вектор u, перпендикулярный
всем этим векторам, и все эти точки ![]() лежат на плоскости с
уравнением (4), проходящей через точку
лежат на плоскости с
уравнением (4), проходящей через точку![]() ,
ортогональной вектору u. Формально принадлежность n+1 одной точки к
плоскости записывают в виде равенства нулю определителя:
,
ортогональной вектору u. Формально принадлежность n+1 одной точки к
плоскости записывают в виде равенства нулю определителя: 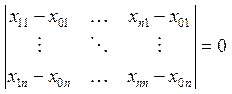 (10)/
(10)/
Определение. Углом между двумя плоскостями называется тот из углов между векторами нормали этих
плоскостей, который![]() . Угол
. Угол ![]() между
плоскостями с векторами нормали u и v находится по формуле:
между
плоскостями с векторами нормали u и v находится по формуле: 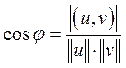 (11).
(11).
22. Расстояние от точки до плоскости. Расстояние между параллельными плоскостями.
Определение. Будем называть расстоянием от точки до плоскости минимальное расстояние от данной точки до точек m-плоскости.
Т.к. минимальное расстояние от данной точки до точек всякой прямой, лежащей на m-плоскости, является расстоянием от данной точки до основания перпендикуляра, опущенного из нее на прямую. Расстояние от точки до m-плоскости равно расстоянию от этой точки до основания перпендикуляра, опущенного из нее на m-плоскость.
Найдем расстояние от точки ![]() до
плоскости, заданной уравнением
до
плоскости, заданной уравнением ![]() (4). Уравнение
перпендикуляра, опущенного из точки
(4). Уравнение
перпендикуляра, опущенного из точки ![]() на плоскость имеет вид:
на плоскость имеет вид:
![]() (12). Подставим (12) в (4):
(12). Подставим (12) в (4):![]() .
. 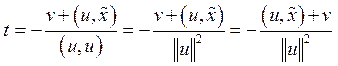 (13).
Т.к. расстояние
(13).
Т.к. расстояние ![]() от точки
от точки ![]() до
произвольной точки плоскости равно
до
произвольной точки плоскости равно 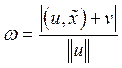 (14). В
частности расстояние до плоскости от начала системы равно
(14). В
частности расстояние до плоскости от начала системы равно 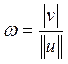 (15). Когда вектор нормали
единичный, формулу (14) можно записать, как
(15). Когда вектор нормали
единичный, формулу (14) можно записать, как ![]() (14’),
а (15):
(14’),
а (15): ![]() (15’). В случае, когда
вектор нормали единичный, абсолютная величина свободного члена в (4)
равна расстоянию до плоскости.
(15’). В случае, когда
вектор нормали единичный, абсолютная величина свободного члена в (4)
равна расстоянию до плоскости.
Утверждение. Поскольку
у параллельных плоскостей могут быть выбраны одни и те же направляющие векторы![]() , то векторы нормали параллельных
плоскостей коллинеарны. Расстояния от всех точек одной из двух параллельных
плоскостей до другой из этих плоскостей равны. Действительно, расстояние от
произвольной точки
, то векторы нормали параллельных
плоскостей коллинеарны. Расстояния от всех точек одной из двух параллельных
плоскостей до другой из этих плоскостей равны. Действительно, расстояние от
произвольной точки 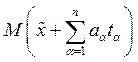 к плоскости, проведенной через
точку
к плоскости, проведенной через
точку ![]() параллельно данной плоскости (4) с
направляющими векторами
параллельно данной плоскости (4) с
направляющими векторами![]() , в силу (14) равно
, в силу (14) равно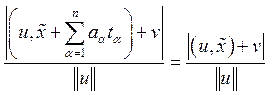 . Т.е. равно расстоянию
. Т.е. равно расстоянию ![]() от точки
от точки ![]() до той
же плоскости.
до той
же плоскости.
Определение. Будем называть число, равно этим расстояниям, расстоянием между двумя параллельными плоскостями.
Если уравнения двух плоскостей записаны в виде: ![]() (17), то расстояние между ними равно
расстоянию от точки
(17), то расстояние между ними равно
расстоянию от точки![]() , лежащей на второй плоскости до
первой. В силу соотношения (14), это расстояние равно
, лежащей на второй плоскости до
первой. В силу соотношения (14), это расстояние равно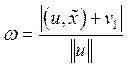 , но т.к. точка
, но т.к. точка ![]() лежит
на второй плоскости, то вектор
лежит
на второй плоскости, то вектор ![]() удовлетворяет уравнению
этой плоскости, т.е.
удовлетворяет уравнению
этой плоскости, т.е.![]() . Получаем:
. Получаем: 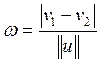 (18).
(18).
23. Приведение уравнения кривой второго порядка к каноническому виду с классификацией возможных типов типов в случае δ≠0
Зафиксируем на плоскости прямоугольную
систему координат и рассмотрим общее уравнение второй степени.(1) ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.