Билинейные формы в вещественном линейном пространстве. Матрица билинейной формы и ее преобразование при изменении базиса. Приведение квадратичной формы к сумме квадратов методом Якоби. Закон инерции квадратичной формы. Ранг квадратичной формы, страница 5

11.  Доказать, что а) характеристический многочлен не зависит от выбора базиса; б) система собственных векторов, соответствующих попарно различным собственным значениям, линейно независима; в) собственные векторы линейного оператора, соответствующие одному собственному значению, вместе с нулевым вектором образуют подпространство. Связь между линейными операторами и билинейными формами в унитарном пространстве.

Определение. Многочлен, стоящий в левой части уравнения  называется характеристическим многочленом матрицы оператора А, а само уравнение называет характеристическим или вековым уравнением этой матрицы.

Теорема 2. Характеристический многочлен не зависит от выбора базиса.

Доказательство. Зафиксируем в пространстве Х некоторый базис  и обозначим через  матрицу оператора А в этом базисе. Пусть в некотором базисе  оператор имеет матрицу. Тогда.

Теорема 3. Если линейный оператор А имеет n линейно независимых векторов (является оператором простой структуры), то, выбрав их в качестве базиса линейного пространства, мы приведем матрицу линейного оператора к диагональной форме. Обратно, если в некотором базисе матрица линейного оператора диагональна, то все векторы этого базиса являются собственными векторами.

Доказательство. Пусть А – линейный оператор, который имеет n линейно независимых векторов, где  и пусть  - его линейно независимые собственные векторы:. Выберем, как базис Х. В этом базисе матрица оператора будет диагональной, на диагонали будут собственные значения.

Теорема 4. Система собственных векторов, соответствующая попарно различным собственным значениям, линейно независима.

Доказательство. (через математическую индукцию).

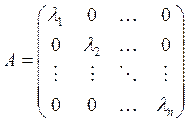
1.  n=1. Т.е.. Теорема верна.

2.  Пусть теорема верна для n-1 векторов, т.е. линейно независимы.

3.  Докажем, что теорема верна для n векторов (от противного):
 (4) - не все коэффициенты в этой линейной комбинации ненулевые. Пусть..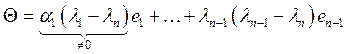 Имеем нулевую комбинацию линейно независимых векторов, а значит и противоречие.

Теорема 5. Если характеристический многочлен линейного оператора А имеет n различных корней, то матрица линейного оператора А может быть приведена к диагональной форме.

Доказательство. Каждому корню  характеристического уравнения отвечает хотя один собственный вектор. Т.к. у этих собственных векторов собственные значения различны, то по теореме 4 мы имеем n линейно независимых векторов. Если эти векторы принять за базис, то матрица линейного оператора А в нем будет диагональной.

Теорема 6. Собственные векторы линейного оператора А, соответствующие собственному значению, вместе с нулевым вектором образуют подпространство пространства Х.

Доказательство. Пусть  - два собственных вектора линейного оператора А, соответствующие одному собственному значению. Нужно показать, что  - тоже собственный вектор:. Указанное подпространство, порожденное собственным значение, является ядром оператора.

Утверждение. Всякому линейному оператору А в линейном пространстве с определенным скалярным произведением отвечает билинейная форма, задаваемая соотношением:.

Проверка на корректность:

1) 

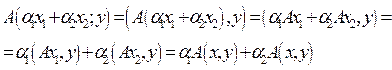
2)  .

Проверка на однозначность:

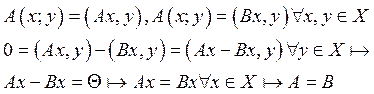
Утверждение. Каждой билинейной форме в линейном пространстве со скалярным произведением отвечает линейный оператор А такой, что:.

12.  Операция перехода от оператора A к сопряженному. Свойства операции. Нахождение матрицы сопряженного оператора в ортонормированном (ортогональном) базисе.

Нахождение матрицы сопряженного оператора в ортонормированном базисе. Пусть в линейном пространстве Х выбран ортонормированный базис  и.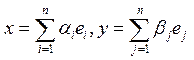

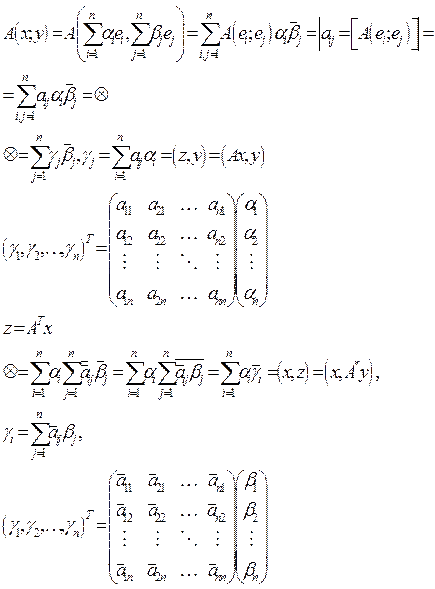
Матрица сопряженного оператора

Теорема 1. Формула  (1) устанавливает в линейном пространстве со скалярным произведением взаимно однозначное соответствие между билинейными формами и линейными операторами. Связь между ними можно установить также другим способом. При этом матрица линейного оператора  получается из матрицы оператора А в ортонормированном базисе путем транспонирования и комплексного сопряжения ее элементов.