Расчет и проектирование рельсовой колеи для движения грузовых поездов со скоростью 65км/ч, страница 7

N – знаменатель марки крестовины;

l_н – длина накладки (800мм);

x – расстояние от торца накладки до оси первого болтового отверстия (80 мм);

δ – величина стыкового зазора( δ=0).

n = (150 – 75 + 175)·15,5 + 0,5·800 – 80 – 0,5·0=4195мм

m = (B + b + Δ)·N

где  Δ – зазор между подошвами рельсов примыкающих к сердечнику 5мм.

m = (150 + 75 + 5)·15,5 = 3565мм

l_к =4195+3565=7760мм

2.2.3 Практическая длина крестовины

Практическую длину определим исходя из равномерного распределения брусьев под крестовиной. При этом необходимо соблюсти ряд условий:

1.  Пролёты между осями шпал должны составлять на прямой 545мм, а на кривых менее 1200–500мм

2.  Брусья под крестовиной располагаются так, чтобы сечение сердечника, размером 20мм находилось в середине пролёта.

3.  Брусья под крестовиной укладывают перпендикулярно биссектрисе α

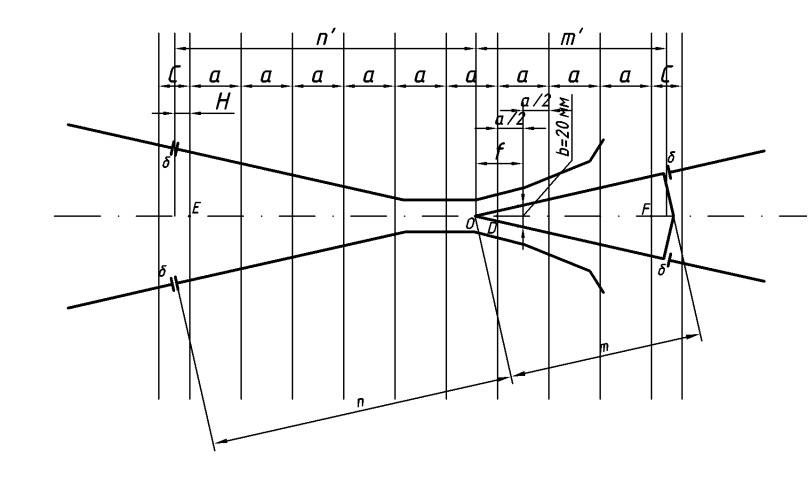
Рисунок 2.7 – Раскладка брусьев под крестовиной

Сечение сердечника размером 20мм находится на расстоянии f от центра крестовины и составляет:

                                 (2.28)                                         

Найдем проекции величин m и n на биссектрису угла α:

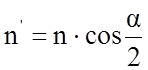                                 (2.29)

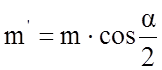                                 (2.30)

Ось первого бруса от переднего стыка крестовины располагается на расстоянии H:

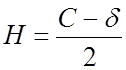                                  (2.31)

где  С – стыковой пролёт (С = 420мм)

δ – стыковой зазор(δ = 0 мм)

 Для распределения брусьев под передней частью крестовины найдем расстояние ED:

ED = n^’ – H + f – 0,5·a                                                       (2.32)

где а – величина пролёта (а = 500мм)

ED = 4192,82 – 210 + 310,32 – 0,5·500 =4043,14мм

Отсюда число пролётов на этом участке будет равно:

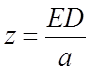                              (2.33)

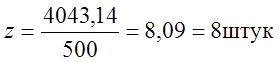
Так как z удлинилась в большую сторону то пересчитаем её проекцию заново:

                                                              (2.34)

Отсюда найдем практическое значение передней части крестовины:

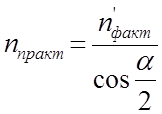                                        (2.35)

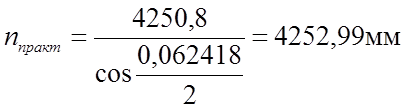
Для дальнейших расчетов n = n_практ

Аналогично определим длину хвостовой части крестовины:

DF=m^’ – h – f + 0,5a                              (2.36)

DF=3563,15 – 210 – 310,32 + 0,5·500 = 3292,83мм

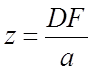                                  (2.37)

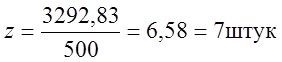
=H + z·a + f – 0,5a                                       (2.38)

= 210 + 7·500 + 310,32 – 0,5·500 = 3770,32мм

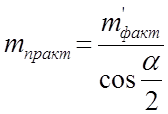                                              (2.39)

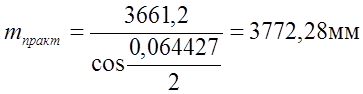
Длина крестовины:

                                           (2.40)

2.3 Определение основных параметров эпюр стрелочного перевода

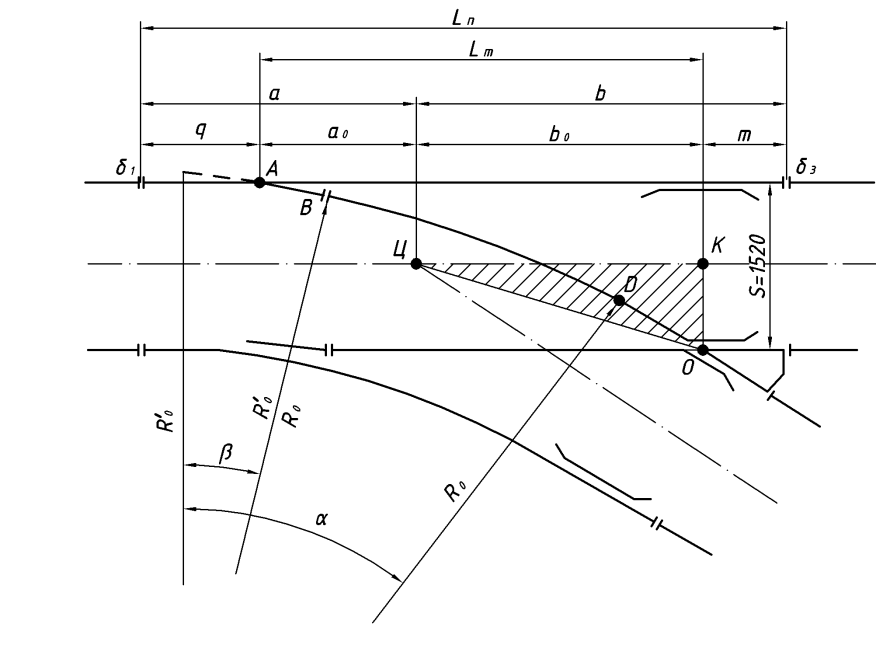
Рисунок 2.8 – основные геометрические размеры стрелочного перевода

2.3.1 Теоретическая длина стрелочного перевода

Теоретической длиной стрелочного перевода называют расстояние от начала остряков до математического центра крестовины:

L_т= ·(sinξ – sinβ_н) + R₀·(sinα – sinξ) + d·cosα                                                   (2.41)

L_т= ·(0,016372  – 0,0068556) + ·(0,064382 – 0,016372) + 5861,4·0,997925 + 5849,2 = 38640мм

2.3.2 Практическая длина крестовины

Практической длиной крестовины называется расстояние от оси зазора в переднем стыке рамного рельса до оси зазора в заднем стыке крестовины:

L_п = q + L_т + m +                                                (2.42)

где δ – величина стыкового зазора (мм)

q – величина переднего вылета рамного рельса

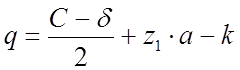                                                   (2.43)

где a – величина пролёта (500мм);

С – стыковой пролёт (420мм)

δ – зазор (8мм)

z₁ – число пролётов между осями переводных брусьев в зоне переднего вылета рамного рельса. Для марки 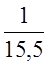 принимаем z₁ = 7шт.

k – смещение начала остряка относительно оси переводного бруса (k = 41мм).

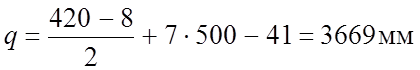
Подставив полученное значение в формулу  (2.42) определим значение L_п:

L_п = 3665 + 38640 + 3772,28 += 46081,28мм

2.3.3 Малые и большие полуоси стрелочного перевода

Расстояние от центра стрелочного перевода до математического центра крестовины определим из прямоугольного треугольника ЦКО [1, рис. 3.19]