Расчет и проектирование рельсовой колеи для движения грузовых поездов со скоростью 65км/ч, страница 3

Рисунок 1.5 – расчетная схема для определения возвышения наружного рельса в кривых

Для уменьшения их воздействия устраивают возвышение наружного рельса

величину возвышения наружного рельса определяют по трем основным критериям :

1.  Условие опрокидывания подвижного состава и равномерный износ рельсов

2.  Условие не превышения непогашенного ускорения для грузовых поездов(непогашенное ускорение для поездов –)

3.  Условие не превышения непогашенного ускорения для пассажирских поездов(условие комфортабельности езды пассажиров)

Согласно положению 2012 года дополнительно находится максимальное значение возвышения:

По первому условию возвышение определяется по формуле (2.0)

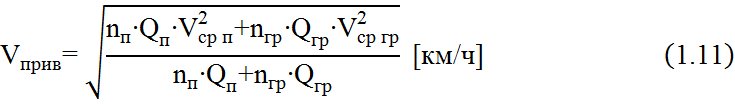
где  V_прив приведенная скорость поездопотока, км/ч

n – число поездов в сутки

Q –  масса поездов в тоннах

V_ср – средняя скорость поездов

По формуле (2.1) подсчитаем V_прив

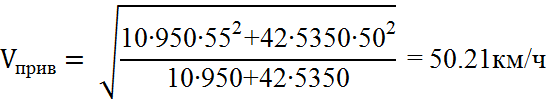
Определим h по формуле (2.0)

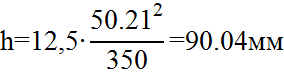
По второму условию возвышение определяется по формуле (2.2)

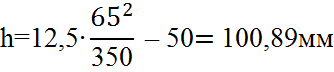
По третьему условию возвышение определяется по формуле (2.3)

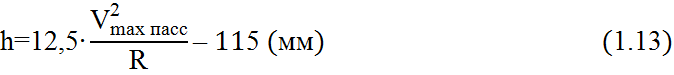
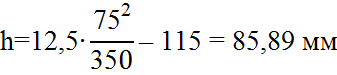
Из полученных величин выбираем большую и округляем кратно 5 в большую сторону( Принимаем 105 мм).

В настоящее время максимальную величину возвышения принято ограничивать 140 мм, поэтому принимаем величину возвышения равной 140 мм.

1.4  Расчет и проектирование переходной кривой и определение элементов для её разбивки

Переходные кривые устраивают для обеспечения плавности входа в кривую,

а также для отвода возвышения и уширения колеи. Радиус переходной кривой меняется от бесконечности до радиуса круговой кривой(Рис. 1.6)

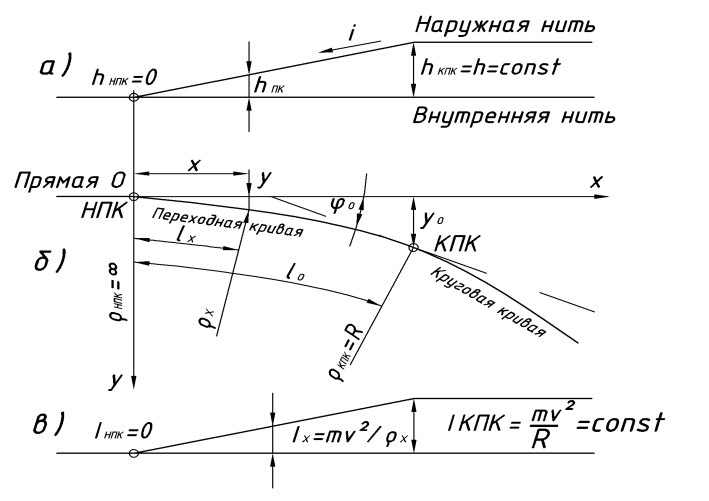
Рисунок 1.6 – Схема переходной кривой

Длину переходной кривой определим по формуле:

где h – возвышение наружного рельса, мм

i – уклон отвода возвышения , мм/м(принимаем уклон равный 0,8мм/м)

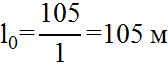
Принимаем l₀= 105м

Проверим возможность разбивки переходной кривой по условию:

где  заданный угол поворота кривой, рад

 угол поворота на протяжении переходной кривой, определяется по формуле:

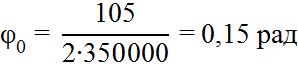
 Так как условие выполняется (2·0,15 < 0,81 ), то мы можем разбить переходную кривую перед круговой

Определим длину круговой кривой по формуле:

Для разбивки переходной кривой на местности найдем её геометрический параметр:

     

Переходная кривая может быть представлена в виде кубической параболы или радиоидальной спирали. Для того чтобы определить вид кривой необходимо проверка условия:

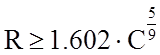
Так как условие не выполняется то переходную кривую примем в виде радиоидальной спирали:

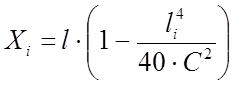                                                  ;                                                                      (1.19)

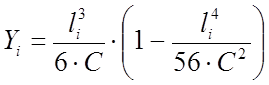                                                                                                                      (1.20)

Расчет будем вести в табличной форме

Таблица 1.5 – Координаты переходной кривой по радиоидальной спирали

li,м	Xi	Yi		li	Xi	Yi
10	10,000	0,002		90	89,809	1,380
20	20,000	0,015		100	99,677	1,894
30	29,999	0,051		110	109,480	2,520
40	39,997	0,121		120	119,197	3,271
50	49,990	0,237		130	128,801	4,158
60	59,975	0,409		140	138,264	5,192
70	69,946	0,650		150	147,549	6,385
80	79,894	0,970		160	156,615	7,746

По результатам таблицы построим график :