Расчет и проектирование рельсовой колеи для движения грузовых поездов со скоростью 65км/ч, страница 4

     Рисунок1.7– Координаты переходной кривой

  Определим основные размеры для разбивки переходной кривой

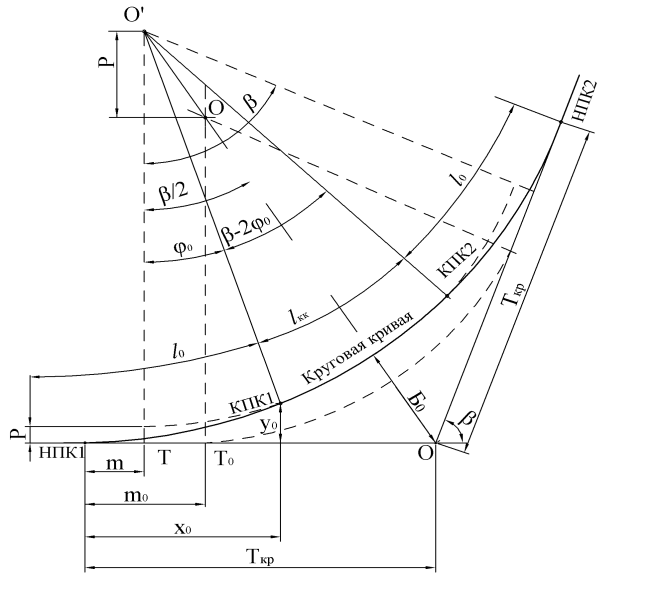
Рисунок1.8 – Схема разбивки переходных кривых методом сдвижки круговой кривой внутрь

Разбивку будем производить методом сдвижки кривой внутрь.

Определим сдвижку по формуле:

                                                      (1.21)

где y_к – конечное значение y_i

Расстояние от начала переходной кривой до первоначального положения тангенсного столбика обозначается m₀ и определяется по формуле:

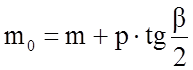                                                (1.22)                                                             

где m – расстояние от начала переходной кривой до нового положения

тангенсного столбика:

                                                (1.23)

где x_к– конечное значение x_i

Подставив полученное значение в формулу (1.22) получим:

Полная длина кривой будет равна:

                                                         (1.24)

Суммированный тангенс новой кривой будет равен:

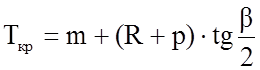                                                   (1.25)

Суммированная биссектриса:

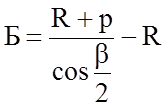                                           (1.26)

Проверка:

Проверка выполняется

Домер:

                                           (1.27)

1.5  Расчет числа и порядка укладки укороченных рельсов на внутренней нити кривой

Определим величину укорочения внутренней нити по отношению к наружной:

                                        (1.28)

где S₀ – расстояние между осями рельсов(1600 мм)

Число укороченных рельсов  необходимых для укладки в путь определим как:

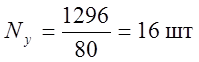                                                (1.29)

где K_i – типовое укорочение рельсов (Так как R=350< 600, то принимаем K=80)

Вычислим общее число звеньев в кривой:

                                           (1.30)

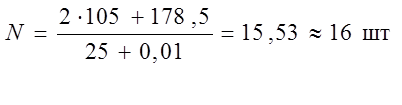
Найдем величины укорочения на переходных кривых:

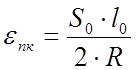                                              (1.31)

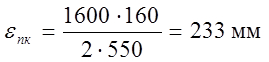
Укорочение круговой кривой:

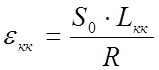                                              (1.32)

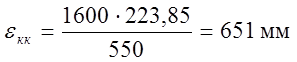
Полное укорочение:

                                              (1.33)

Проверка:

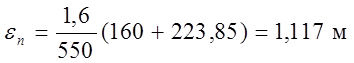                                                         (1.34)

Расчет укорочения будем вести в табличной форме:

Для первой переходной кривой:

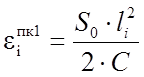                                           (1.35)

Для второй переходной кривой:

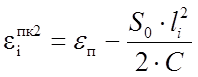                                                (1.36)

Для круговой кривой:

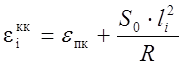                                              (1.37)

Таблица1.6 – Расчет порядка укладки укороченных рельсов по внутренней нити кривой