Проект рельсовой колеи и стрелочного перевода, страница 8

На рисунке 2.7 представлена схема крестовины, у которой передний и задний стыки расположены на весу со стыковым пролетом С.

 

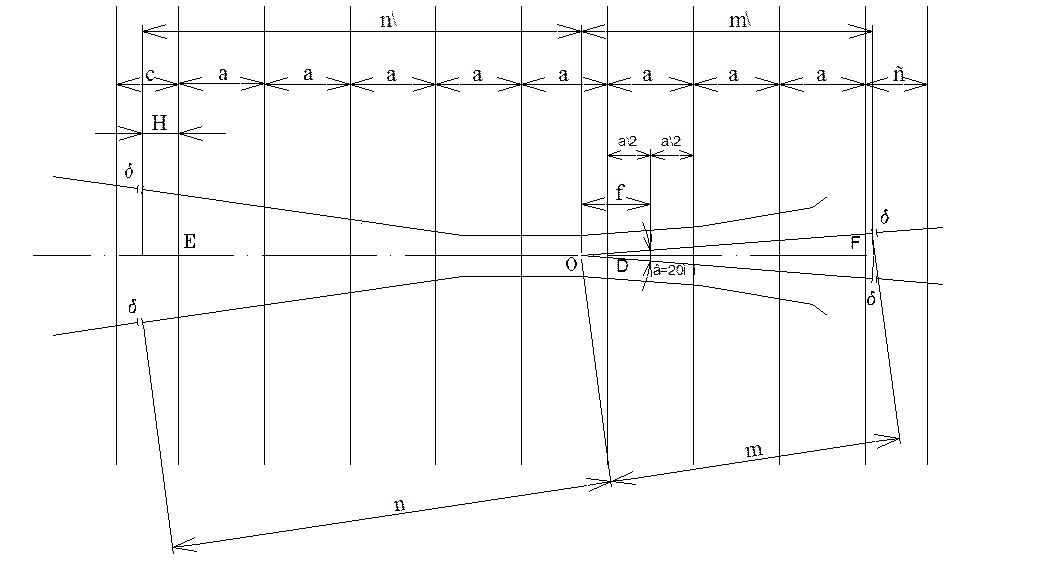
Рисунок 2.7 – Раскладка брусьев под крестовиной

Размеры крестовины   и  по ее оси, то есть проекции величин n и m на биссектрису угла a, определяются следующими выражениями

; ,

(2.31)

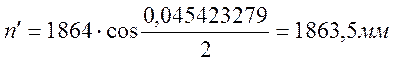
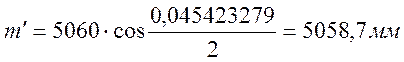
Сечение сердечника шириной b = 20 мм от математического центра крестовины находится на расстоянии

,

(2.32)

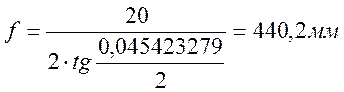
Ось первого бруса от переднего стыка крестовины располагают на расстоянии Н, которое составляет

,

(2.33)

где С - стыковой пролет, мм;

d - размер стыкового зазора.

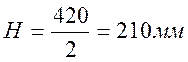
Первый брус под сердечником крестовины в 20 мм от его сечения укладывается на расстоянии 0,5а.

Для распределения брусьев под передней частью крестовины необходимо знать расстояние ЕD (рисунок 2.7), оно определяется из следующего выражения

,

(2.34)

При принятом пролете а число пролетов на участке ЕD будет равно

,

(2.35)

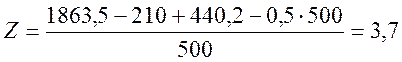
Принимается число пролетов: M=4, что означает удлинение передней части крестовины. При этом фактическая проекция передней части крестовины будет равна

,

(2.36)

а ее  практическая длина

,

(2.37)

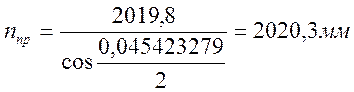
Для определения практической длины хвостовой части крестовины необходимо знать размер DF по ее оси. Из рисунка 2.7 видно

,	(2.38)

где d - величина стыкового зазора.

Число пролетов Z¢ на участке ДF будет

,

(2.39)

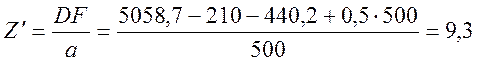
Принимается число пролетов: M^’=10, что означает удлинение хвостовой части крестовины. При этом фактическая проекция хвостовой части крестовины на биссектрису ее угла определяется

,

(2.40)

Практическая длина хвостовой части крестовины будет равна

,

(2.41)

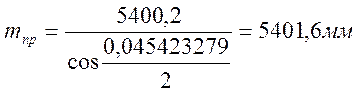
Полная  практическая длина крестовины определится следующим выражением

,

(2.42)

2.3 Определение основных параметров эпюры стрелочного перевода

К основным параметрам эпюры стрелочного перевода относятся: теоретическая и практическая длины стрелочного перевода, большие и малые полуоси.

2.3.1 Теоретическая длина стрелочного перевода

Теоретической длиной стрелочного перевода называется расстояние от начала остряка до математического центра крестовины, которую можно определить из уравнения проекции контура   АВДО на  горизонтальную  ось    (рисунок 2.8)

,

(2.43)

где - радиус остряка в его начальной части, мм;

- радиус переводной кривой, мм;

b_н - начальный угол;

x - угол в конце строжки остряка;

a- угол крестовины;

d - прямая вставка перед математическим центром крестовины, мм.

Рисунок 2.8 – Основные геометрические размеры стрелочного перевода

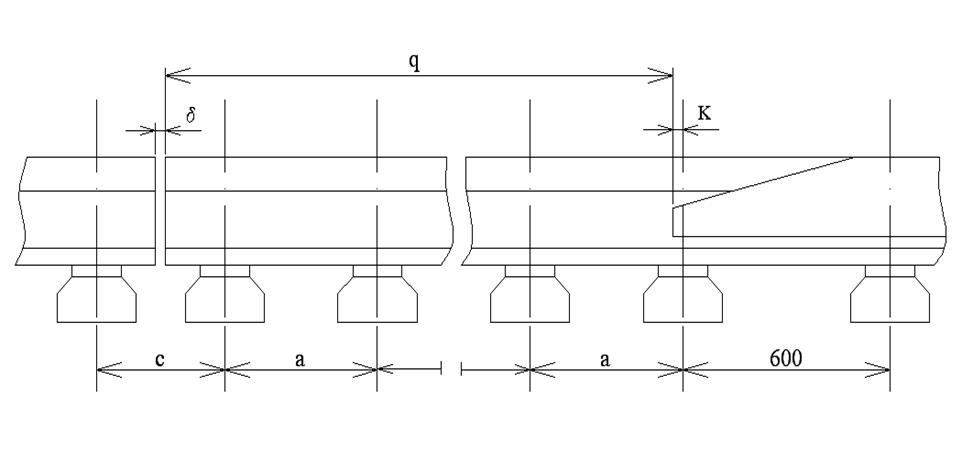
Рисунок 2.9 – Схема к определению длины переднего вылета рамного рельса

2.3.2 Практическая длина стрелочного перевода

Практической длиной стрелочного перевода называется расстояние от оси зазора в переднем стыке рамного рельса до оси зазора в заднем стыке крестовины. Практическая длина стрелочного перевода (рисунок 2.8)

,	(2.44)

где q - передний вылет рамного рельса, мм;

L_т - теоретическая длина стрелочного перевода, мм;

m_пр - практическая длина заднего вылета крестовины, мм;

d₁ - величина стыкового зазора, мм.

Размер переднего вылета рамного рельса q определяется количеством и величиной пролетов между брусьями.

По условиям раскладки переводных брусьев и расположения начала остряка со сдвижкой его относительно оси переводного бруса на величину К (рисунок 2.9) передний вылет рамного рельса определяется зависимостью

,	(2.45)

где С - стыковой пролет, принимаемый в зависимости от типа рельсов;

d - стыковой зазор в переднем стыке рамного рельса;

 а_i - величина пролета (расстояние между осями брусьев) под стрелкой;      

К - смещение начала остряка относительно оси переводного бруса;