Один из способов решения этой задачи - графический. Создаём таблицу из 3 столбцов. В первый столбец занести значения Х от 0 до 16. Во втором столбце выводятся значения Y1 с помощью формулы =(50-4*А118)/3. В третьем столбце выводятся значения Y2 с помощью формулы =14-А118.
На основе полученных результатов построим диаграмму. Диаграммы используются для наглядного представления данных. Многие данные будут более понятными, если изобразить их на диаграмме.
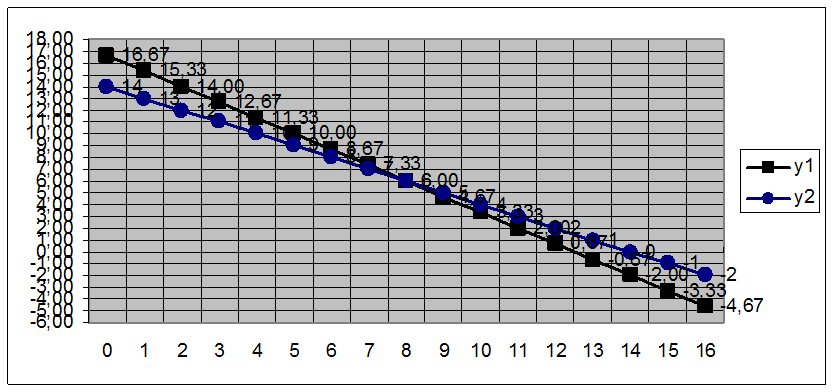
Рис.3 Диаграмма, связанная с данными таблицы
Результаты решений задачи, полученные вышеописанными способами, должны совпадать.
3. Решение задач линейной оптимизации с помощью инструмента Поиск решения
Пример: В частном ателье производя три типа (фасона) костюмов. Затраты на каждый тип костюма составляют: расход материала соответственно 2,5м; 2,7м; 2,4м; дополнительный расход на подклад, нити, пуговицы – 50р., 65р., 45р. Сколько костюмов каждого типа нужно произвести, чтобы прибыль была максимальной, если доход от продажи одного костюма составляет – 200р., 175р., 180р., а стоимость одного метра ткани – 620р. Всего фирма потратила на ткань 25000; на подклад, нити, пуговицы – 1000р.
Решение: Составим математическую модель. Обозначим: хi – количество костюмов i-го типа. Прибыль от продажи костюмов равна 200*х1+175*х2+180*х3. Её нужно максимизировать. Функция, для которой ищется экстремум (максимум или минимум) носит название целевой функции. Беспредельному увеличению количества изделий препятствуют ограничения. Ограничена сумма денег, которую выделили на ткань и дополнительный материал, отсюда два неравенства: 650*(2,5* х1+2,7* х2+2,4* х3)<=25000 и 50* х1+65* х2+45* х3<=1000. Кроме того, количество костюмов не может быть отрицательным, поэтому хi >=0.
Решите эту задачу с помощью ПОИСКА РЕШЕНИЯ.
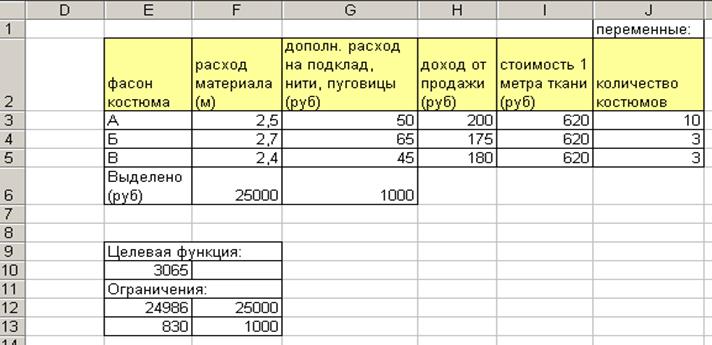
Рис.4. Результаты работы инструмента ПОИСК РЕШЕНИЯ
3-й уровень помощи (подробный)
В EXCEL можно решать задачи отыскания наибольших и наименьших значений, а также решать уравнения. Это позволяет осуществить надстройка «Поиск решения».
1. ИнструментПоискрешения
Инструмент Поиск решения является частью блока задач, который иногда называют анализ «что - если» (анализ «что - если» - процесс изменения значений ячеек и анализа влияния этих изменений на результат вычисления формул на листе). Этот инструмент может применяться для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинации переменных, которые максимизируют или минимизируют значение в целевой ячейке. Он также позволяет задать одно или несколько ограничений – условий, которые должны выполняться при поиске решения.
Инструмент Поиск решения оперирует (действует) со следующими понятиями:
§ Изменяемые ячейки. Значения переменных в ячейках, которые изменяются программой поиск решения для получения заданного значения. Допускается использование до 200 таких ячеек.
§ Ограничения целостности. Ограничения, налагаемые на переменные. Возможно, одни переменные должны быть выражены положительными числами, другие - отрицательными или целыми числами, или же они должны находиться в определённом интервале значений.
§ Целевые ячейки. Ячейки, в которых содержатся заданные значения. Программа поиск решения варьирует (изменяет) значения переменных в изменяемых ячейках для получения заданного значения.
2. Решение систем уравнений с помощью инструмента Поиск решения
В качестве примера задачи, которую позволяет решить Поиск решения, возьмем такую:
Мальчик купил на 50 рублей мороженое двух видов. Мороженое первого вида стоит 4 руб., второго – 3 руб. Сколько мальчик взял мороженого каждого вида, если всего он взял 14 штук?
Для начала составим систему уравнений:
4x+3y=50
x+y=14,
где х – количество мороженого первого вида стоимостью 4 руб.,
у – количество мороженого второго вида стоимостью 3 руб.
Эту задачу можно решить разными способами. Самый простой способ решения подобных задач - ручной, но Поиск решения найдёт решение этой задачи значительно быстрее вас.
Пользуясь этими данными, сначала составьте таблицу:
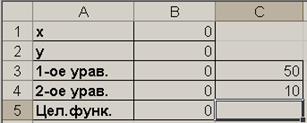
Рис.1. Здесь показан один из способов решения данной задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.