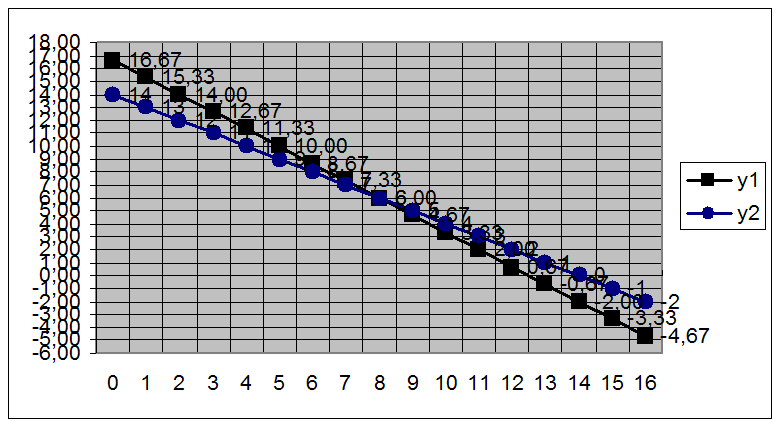
Рис.11. Диаграмма на основе полученных результатов
На диаграмме ясно показано, что оба графика пересекаются в точке (8;6). Значение х равно 8, показывает, что мальчик приобрёл 8 шт. мороженого 1-го вида. Значение у=6, соответственно 6 шт. мороженого 2-го вида. Как видим, решение одной задачи разными способами даёт один и тот же ответ.
В расчётно-графической работе по курсу «Моделирование систем» с помощью инструмента «Поиск решения» можно точно так же найти неизвестные (2 и более) в линейной (или какой-либо другой) модели.
13. Решение задач линейной оптимизации с помощью инструмента Поиск решения
Пример: В частном ателье производя три типа (фасона) костюмов. Затраты на каждый тип костюма составляют: расход материала соответственно 2,5м; 2,7м; 2,4м; дополнительный расход на подклад, нити, пуговицы – 50р., 65р., 45р. Сколько костюмов каждого типа нужно произвести, чтобы прибыль была максимальной, если доход от продажи одного костюма составляет – 200р., 175р., 180р., а стоимость одного метра ткани – 620р. Всего фирма потратила на ткань 25000; на подклад, нити, пуговицы – 1000р.
Решение: Составим математическую модель. Обозначим: хi – количество костюмов i-го типа. Прибыль от продажи костюмов равна 200*х1+175*х2+180*х3. Её нужно максимизировать. Функция, для которой ищется экстремум (максимум или минимум) носит название целевой функции. Беспредельному увеличению количества изделий препятствуют ограничения. Ограничена сумма денег, которую выделили на ткань и дополнительный материал, отсюда два неравенства: 650*(2,5* х1+2,7* х2+2,4* х3)<=25000 и 50* х1+65* х2+45* х3<=1000. Кроме того, количество костюмов не может быть отрицательным, поэтому хi >=0.
Как известно из курса ИО, формально задача оптимизации записывается так:
200*х1+175*х2+180*х3→max
650*(2,5* х1+2,7* х2+2,4* х3)<=25000
50* х1+65* х2+45* х3<=1000
хi >=0.
Теперь решим эту задачу в EXCEL.
Пользуясь данными, сначала создадим таблицу:
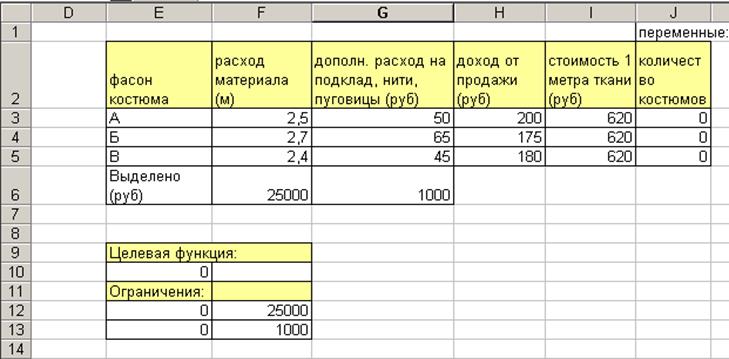
Рис.12. Таблица для вычисления оптимального количества костюмов
В столбцах F, G, H, I содержатся константы: расход материала, дополнительный расход и т.д. для каждого фасона костюмов. Требуется определить количество костюмов каждого фасона (ячейки J3:J5) и максимизировать доход от продажи костюмов.
Ячейка Е10 – это целевая ячейка. В неё записывается целевая функция. В ячейках Е12:Е13 записываем левые части ограничений, а правые части ограничений пишем в соседние ячейки. После этого проделываем все те операции, которые описаны в п. 2-5. Окончательный результат см. ниже:
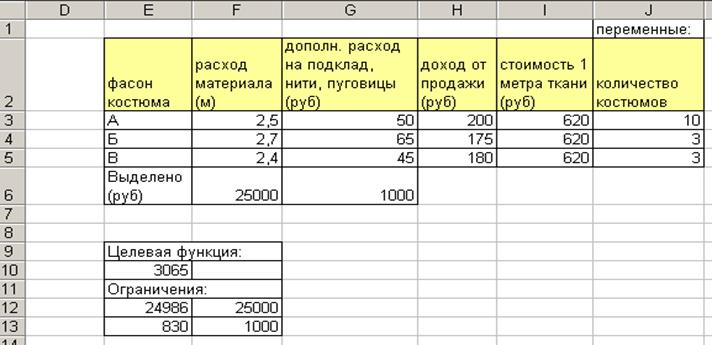
Рис.13 Результаты работы инструмента ПОИСК РЕШЕНИЯ
12. Резюме
Поиск решения позволяет решить как простое линейное уравнение, так и сложную задачу оптимизации
13. Содержание отчёта
2) Задание.
3) Исходные данные.
4) Средства EXCEL, мастера, применяемые при решении задач оптимизации и уравнений.
5) Порядок выполнения задачи (ход работы).
6) Выводы.
14. Условия задач для самостоятельного выполнения
15. Вопросы обучающегося
1) Для решения каких задач применяется инструмент Поиск решения?
16. Глоссарий
Автоматизация процесса подготовки документа
1 уровень помощи (краткий):
Задача:
1. Постановка: Автоматизировать процесс подготовки справки вида:
Выдана [Ф.И.О. студента] и удостоверяет, что [он/она]
является студент[ом/кой] НГТУ факультета [какого] группы [какой].
Справка дана для предъявления [куда].
зам. декана [Ф.И.О. декана].
дата [сегодня].
Рис.1. Справка
В квадратных скобках приведены сведения, которые меняются при необходимости. Для ускорения подготовки справки нужно создать таблицы, где приведены сведения о студентах института, о деканах факультетов, местах, куда требуется предъявить справку, о факультетах, существующих в институте, - словом, вся информация, необходимая для составления справки.
2. Исходные данные:
Для решения поставленной задачи необходимо ввести на рабочем листе, которому для удобства присвоим имя «Справка»:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.