Обработка и фильтрация изображений. Особенности изображений как информационных процессов. Типы помех и искажений, их свойства и модельные представления, страница 16

При обработке многоканальных (цветных и мультиспектральных оптических, а также радиолокационных) изображений можно и часто целесообразно применять векторные нелинейные фильтры.  Достоинством использования векторной обработки данных является то, что многомерное представление сигнала позволяет учесть корреляцию между данными, и в то же время векторные нелинейные фильтры (в основном) сохраняют свойства, присущие их скалярным аналогам.

            Представим отсчеты p-канального изображения в виде вектора

                                              ,       (14.23)

где n₁ и n₂ - номера строки и столбца многоканального изображения.

            Первым из нелинейных фильтров в рассмотрение был введен векторный медианный фильтр. Операция нахождения векторной медианы (ВМ) предусматривает выбор такого вектора  в окне W (выборке), для которого

      ,                                             (14.24)

где  обозначает норму L, N_W - количество отсчетов в окне данных. Оптимальная норма L выбирается в зависимости от ПРВ помех. Для гауссова шума L соответствует возведенному в квадрат евклидову расстоянию, а для распределения Лапласа - линейному расстоянию. В этом случае обеспечивается и большая устойчивость к воздействию импульсных помех.

Отметим, что выходной сигнал векторного нелинейного фильтра является векторным функциональным преобразованием  входного вектора, что не равнозначно применению функционального преобразования Fраздельно к каждому компоненту вектора. Иными словами, в случаях применения к многоканальному изображению векторного медианного фильтра и покомпонентно обычного медианного фильтра при одном и том же окне W результаты фильтрации отличаются.  

Аналогично скалярным фильтрам на основе порядковых статистик можно сортировать (ранжировать) и вектора. Отличие состоит в том, что вектора ранжируются в соответствии со значениями суммарных расстояний от каждого вектора до других векторов. Можно также ранжировать вектора и в зависимости от их расстояния от векторной медианы выборки. Используемый метод ранжирования при этом специально оговаривается. Отметим, что в отличие от скалярного случая, для отсортированной выборки векторных данных векторная медиана является первым (по порядку) элементом. 

Над упорядоченным таким образом рядом векторов в зависимости от типа нелинейного фильтра применяют соответствующие операции. Например, возможны такие операции с векторными данными, как взвешенное усреднение векторных порядковых статистик, исключение из выборки порядковых статистик с наибольшими рангами и последующее усреднение векторов и др. В частности, для векторного a-урезанного фильтра выходной сигнал определяется выражением

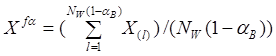                                           (14.25)

где  - l-я векторная порядковая статистика,  - параметр усечения.                                 

Свойства векторного медианного фильтра, векторного a-урезанного фильтра и других векторных фильтров на основе порядковых статистик определяются размером скользящего окна и видом используемой нормы. Во многом они подобны свойствам соответствующих скалярных аналогов. 

Однако векторы можно сортировать не только учитывая суммарные расстояния аналогично (14.24), но и направления векторов. На использовании этого принципа основывается другой класс векторных нелинейных фильтров – векторные направленные (directional) фильтры (ВНФ). В качестве критерия ранжирования векторов в пределах окна фильтра используется угловая мера подобия i-го вектора другим векторам, определяющая различие между ориентацией векторов в p-мерном пространстве. ВНФ применяются для обработки цветных изображений и других векторных данных, когда основной задачей является сохранение цвета или направления векторов (фазовой информации).

Хорошее сохранение деталей и малоразмерных объектов обеспечивается векторным сигма-фильтром.