Обработка и фильтрация изображений. Особенности изображений как информационных процессов. Типы помех и искажений, их свойства и модельные представления, страница 14

2)  Единственным средством уменьшения d (повышения эффективности подавления пространственно-коррелированных помех) является увеличение размера скользящего окна по сравнению с рекомендованным для случая пространственно-коррелированного шума,  однако при этом необходимо помнить, что для всех ПШФ это неизбежно приводит к возрастанию степени искажений в окрестностях границ, малоразмерных объектов и на текстурных участках; в этом плане наиболее привлекателен МСФ с размерами скользящего окна 7х7 или 9х9, для которого при увеличении NxNспособность сохранять границы и детали практически не ухудшается.

Все перечисленные выше фильтры не приводят к специфическим эффектам при их применении для случаев гауссовых аддитивных или мультипликативных помех. При одновременном воздействии импульсных помех могут наблюдаться смещенность среднего уровня выходных значений для однородных участков изображений и заметное увеличение дисперсии остаточных флуктуаций  по сравнению со случаем . Степень проявления этих эффектов зависит от характеристик импульсных помех, робастности и размера скользящего окна фильтра.

Особым является случай мультипликативных помех с  негауссовой ПРВ, например, ПРВ Рэлея или односторонней экспоненциальной, которые характерны для когерентных СФИ. В этих случаях даже при  применение МФ, ЦВМФ, АУФ (14.18) и фильтра Вилкоксона приводит к заметной смещенности среднего уровня выходных значений для однородных участков, что может привести к систематическим погрешностям при решении обратных задач (определения параметров объектов по изображениям) на этапе интерпретации. Для устранения указанного недостатка можно использовать поправочные коэффициенты, то есть, например, для МФ формировать выходное изображение в виде . При этом для предварительного определения  необходимо априорно и с достаточной точностью знать ПРВ мультипликативных помех. В некоторых случаях  для каждого конкретного нелинейного фильтра может быть либо рассчитан аналитически, либо получен методами численного моделирования.

Таким образом, несмотря на большое количество различных неадаптивных нелинейных фильтров, а в данном подразделе кратко рассмотрены лишь некоторые из них, достижение приемлемого компромисса свойств однопроходных фильтров остается проблематичным, хотя в некоторых конкретных ситуациях упомянутые и другие известные нелинейные фильтры могут вполне удовлетворить пользователей.    

14.6. Фильтры на основе ортогональных преобразований и векторные фильтры

Фильтры на основе ортогональных преобразований (прежде всего, дискретном косинусном и разнообразных вейвлетных преобразованиях) также могут быть отнесены к классу нелинейных, поскольку наряду с линейными преобразованиями, используемыми на первом и третьем шагах, на втором шаге используется нелинейная операция сравнения с порогом и либо обнуления, либо преобразования спектральных коэффициентов (см. подраздел 13.1). В приложении к обработке изображений фильтрация для всего изображения или для заданного фрагмента (блока) осуществляется в три этапа:

1)  Расчет двумерного спектра с использованием заданного прямого ортогонального преобразования;

2)  Применение пороговых операций к полученным спектральным коэффициентам;

3)  Выполнение обратного двумерного (дискретного) ортогонального преобразования.        

Эти шаги описывают общую структуру алгоритма. В остальном возможны различные варианты: применение пространственно-инвариантной фильтрации (с циклическим сдвигом изображений или перекрытием блоков), использование жесткого или мягкого порога и т.д. (см. более подробно в подразделе 13.1). В частности, если двумерное дискретное косинусное преобразование применяется для kl-го блока, то получаемый двумерный ДКП спектр W_kl(m,n), m=0, …,M_b-1; n=0,…,N_b-1 описывается выражениями

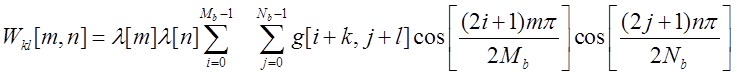,         (14.21)

где  и  - весовые функции вида