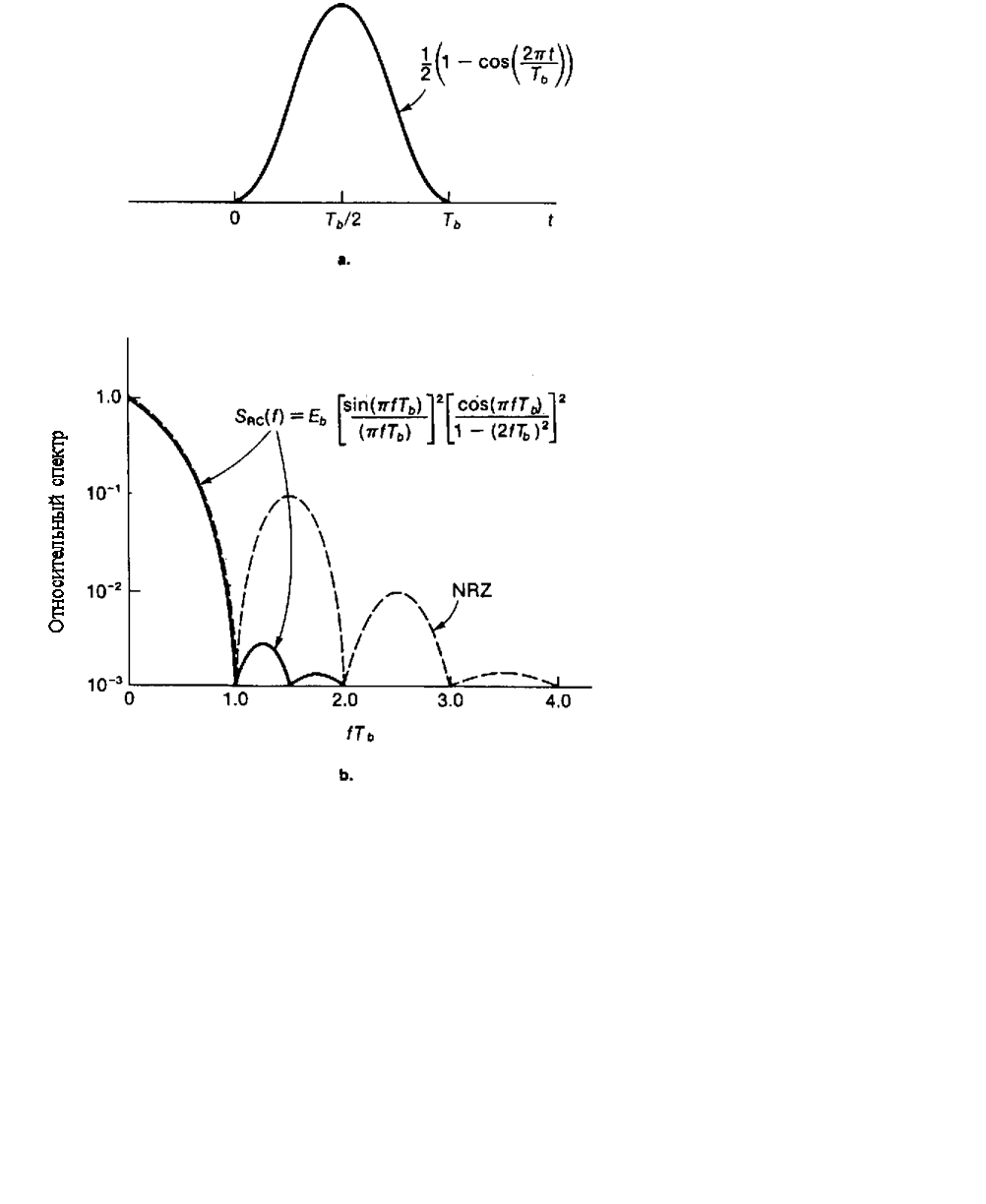
 |
Рис. 2. 10. Функция типа “косинус на пьедестале”.
а) Временная область.
b) Частотная область.
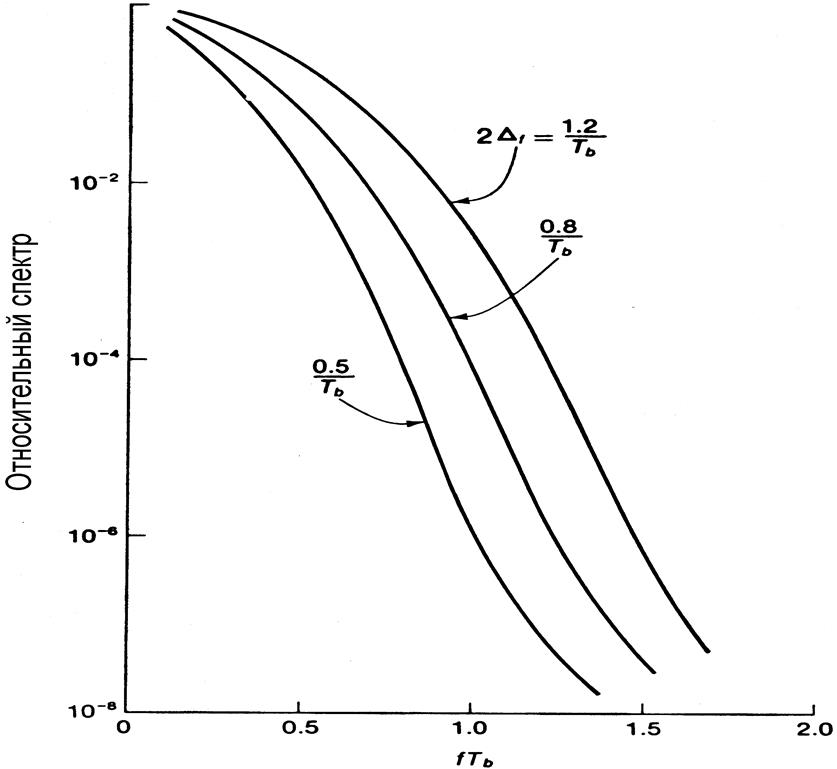
Рис. 2. 11. Спектр пилот-сигнала при частотной манипуляции с использованием сглаживания функцией “косинус на пьедестале”. (Δf = девиация частоты).
Рисунок 2.11 иллюстрирует уменьшение ширины полосы спектра в зависимости от девиации частоты по отношению к полосе спектра при стандартной частотной и двухпозиционной фазовой манипуляции.
Важным свойством пилот-сигнала с частотной манипуляцией является то, что его фаза соответствует непрерывной траектории во времени в соответствии с порядком следования модулирующих данных, как это представлено на рис. 2. 12. Напомним, что фаза пилот-сигнала – это интеграл ЧМ сигнала.
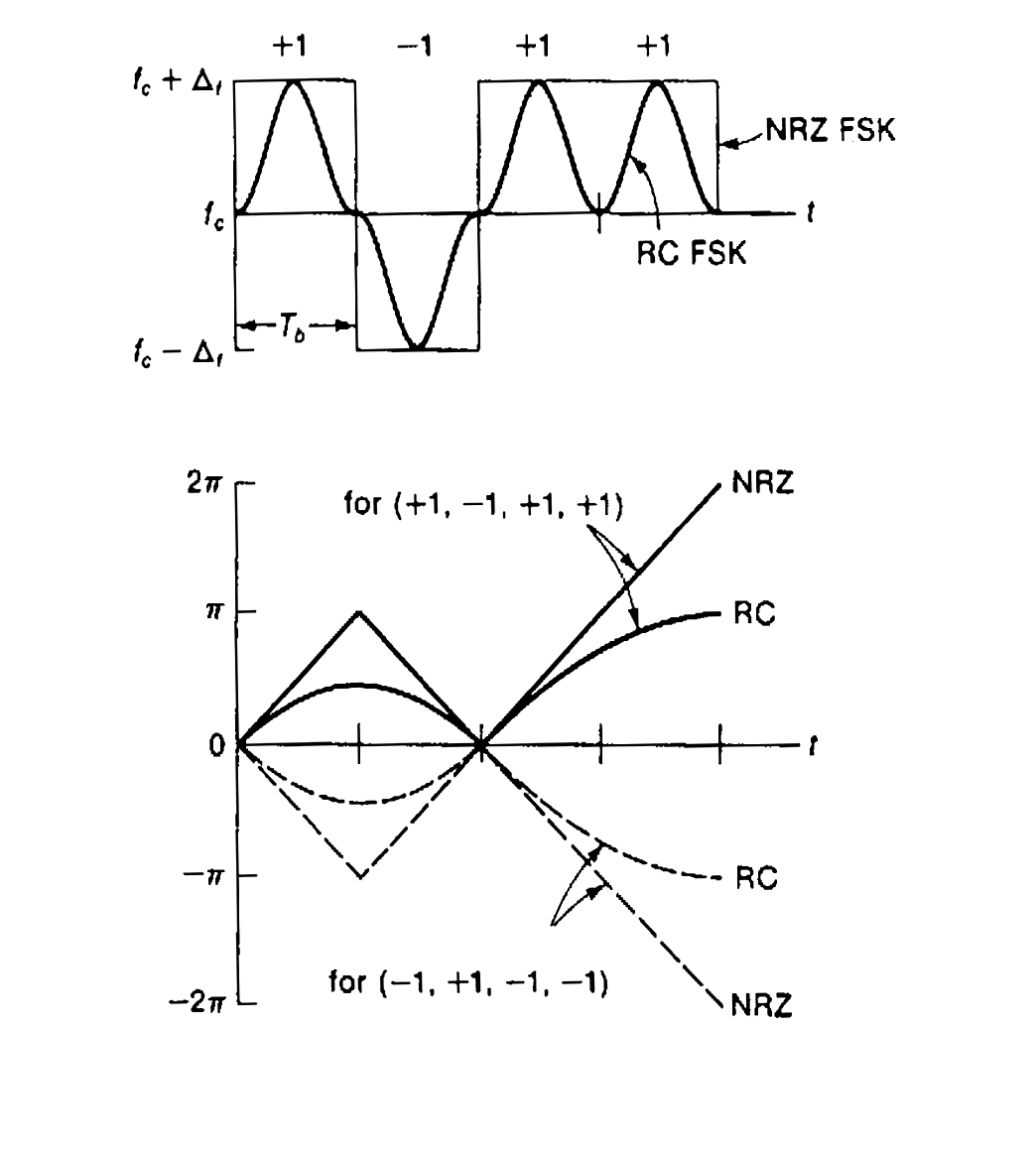
Рис. 2. 12. Изменение частоты и фазы пилот-сигнала при частотной манипуляции (FSK) (NRZ = однополярные модулирующие импульсы прямоугольной формы; RC = модулирующие импульсы типа косинус на пьедестале).
Вследствие того, что фаза пилот-сигнала – это интеграл данного ЧМ сигнала, можно использовать фазовую демодуляцию, отслеживая фазовые функции. По этой причине цифровые ЧМ пилот-сигналы данного типа относят к сигналам с частотной манипуляцией с непрерывным изменением фазы (CPFSK – continuousphaseFSK).
Траектории фазы зависят от формы частотно-модулирующего импульса, а разнос между двумя различными траекториями зависит от девиации частоты Δf . При использовании сглаживающей функции типа «косинус на пьедестале» фазовые траектории становятся более сжатыми и труднее различимыми (см. рис. 2. 12).
Поэтому, хотя уменьшение девиации частоты и приводит к уменьшению ширины основного лепестка спектра (см. рис. 2. 11), при этом, однако, ухудшается способность декодирования посредством отслеживания изменений фазы или посредством непосредственного частотного детектирования.
Дальнейшее уменьшение полосы частот спектра пилот-сигнала при частотной манипуляции (FSK) с использованием сглаживающей функции «косинус на пьедестале» может быть выполнено при увеличении временной протяженности сглаживающей функции при одновременном сохранении скорости передачи двоичных данных.
На рис. 2. 13а показаны несколько сглаживающих функций, длительность которых увеличена до нескольких бит. С увеличением длительности сглаживающих функций уменьшается ширина спектра, как это видно из рис 2. 13б. Однако, если протяженность сглаженного импульса увеличивается до нескольких битовых тактов, возникают помехи из-за взаимного влияния символов (межсимвольные помехи), когда фаза из одного периода бита накладывается на фазы соседних периодов. В результате ухудшаются характеристики фазовой демодуляции.
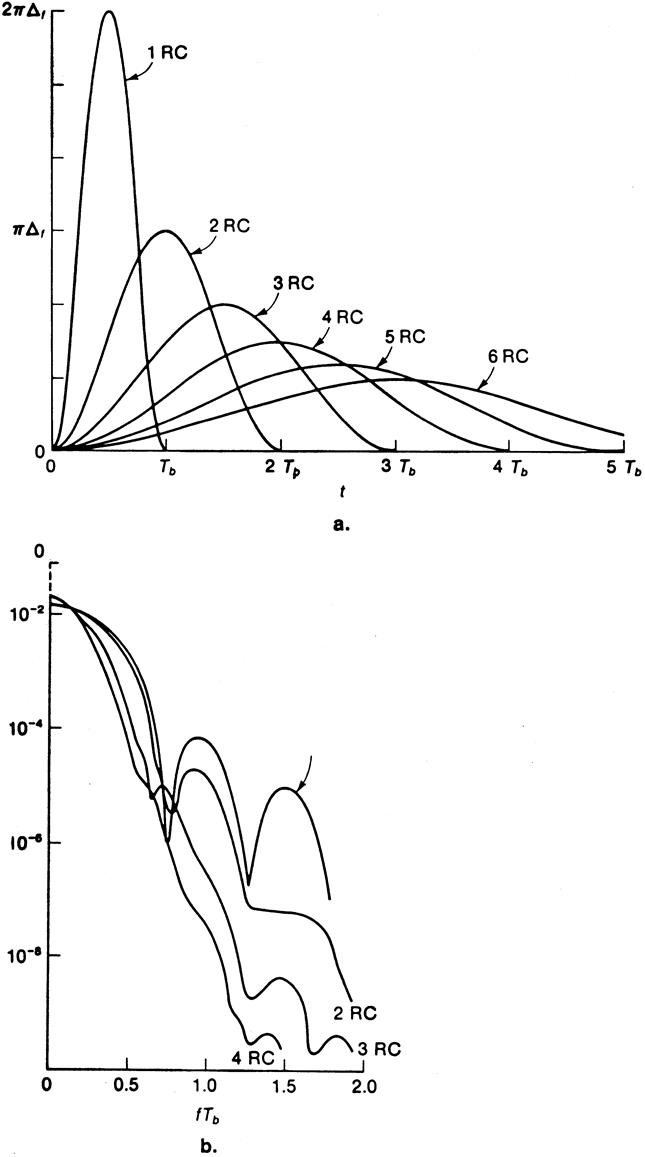
Рис. 2. 13. Сглаживающие функции различной протяженности.
а) Временные сигналы. b) Нормированные cпектры пилот-сигналов при временных сигналах разной протяженности (RC = модулирующие импульсы типа косинус на пьедестале; NRZ = модулирующие импульсы прямоугольной формы – график обозначен стрелкой).
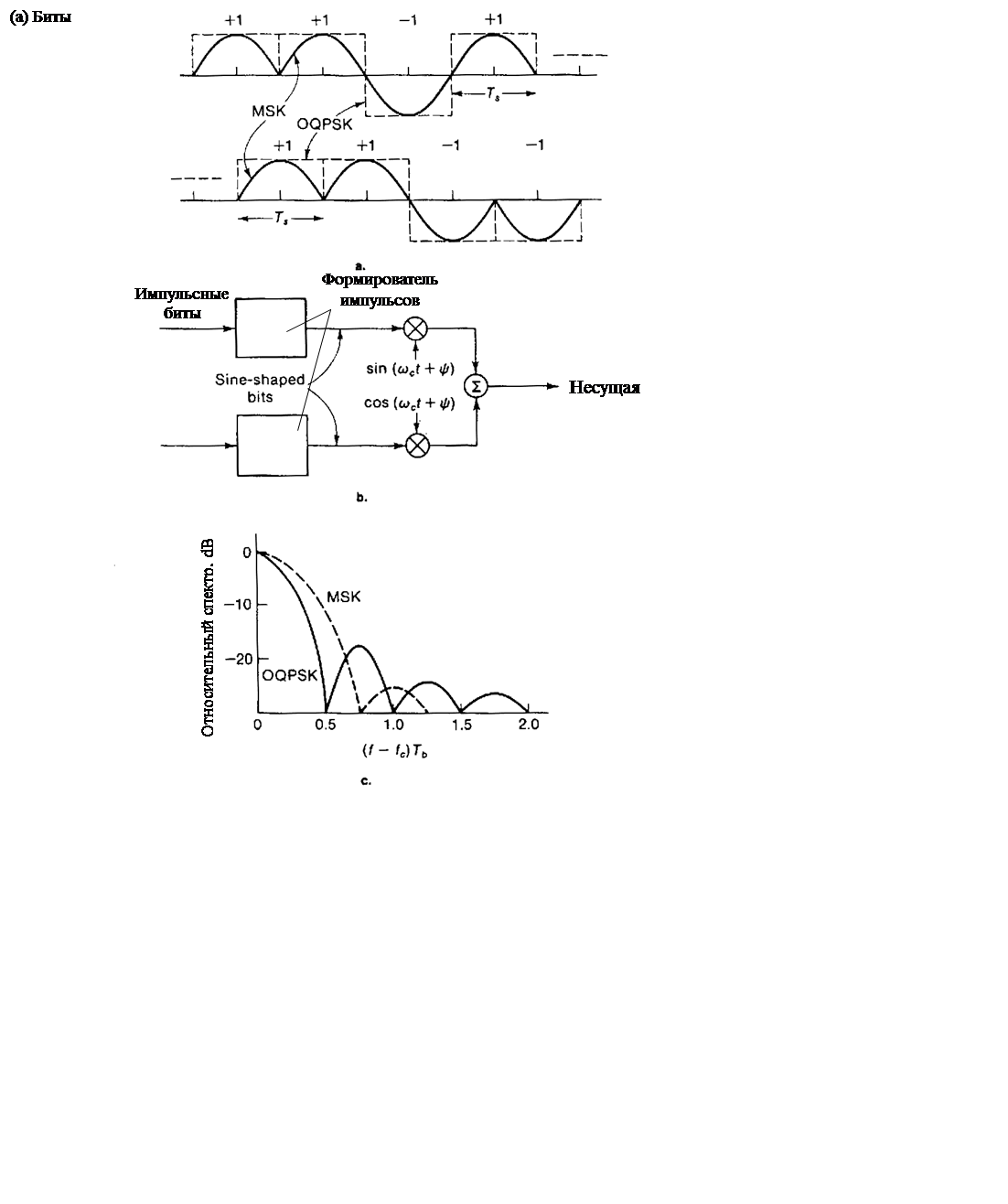
В случае квадратурной фазовой манипуляции (QPSK) использование импульсов, форма которых отличается от прямоугольной, приводит к непостоянству амплитуды огибающей пилот-сигнала. Однако, смещение позволяет, используя фильтрацию импульсов, сохранять огибающую на постоянном уровне. Примером квадратурной фазовой манипуляции (QPSK) и квадратурной фазовой манипуляции со сдвигом (ОQPSK) и фильтрацией является класс пилот-сигналов с манипуляцией минимальным сдвигом (minimumshift-keyed (MSK) carriers). В этом случае используется формат квадратурной фазовой манипуляции ОQPSK, при котором прямоугольные импульсы заменены полупериодами синусоидальных волн (см. рис. 2. 14а). MSK пилот-сигнал генерируют с помощью квадратурных перемножителей (рис. 2. 14б).
Модулирующие функции при этом равны
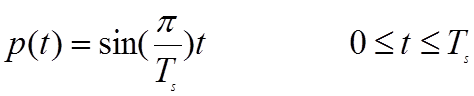(2.4.2а)
и
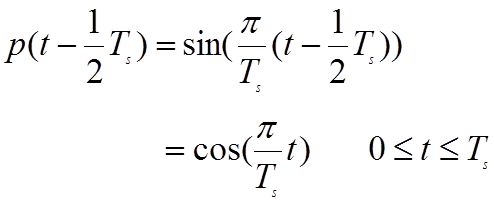. (2.4.2б)
Пилот-сигнал при манипуляции минимальным сдвигом (MSK) имеет вид
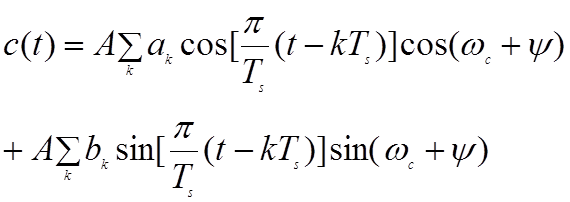. (2.4.3)
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.