Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 2: "Модуляция, кодирование и декодирование", страница 16

Рис. 2. 28. Производительность цифровой системы (R/B) в зависимости от требуемого отношения сигнал/шум (PE=10^-5).

При сложной частотной манипуляции также передают log₂M бит каждые T_w секунд, однако требуемое увеличение ширины полосы частот равно M(2/T_w). Следовательно,

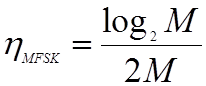                                                                                  (2.8.6)

и производительность при сложной частотной манипуляции уменьшается при увеличении М, достигая максимальной величины 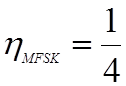 при М=2 и М=4.

Сужение полосы частот с помощью соответствующего изменения формы импульса при частотно-модулированном способе кодирования увеличивает производительность, однако при этом требуется сложная система декодирования, а также увеличение мощности несущего колебания для преодоления межсимвольной интерференции. На графике, представленном на рис. 2.28 отмечены точки для сглаживающей функции «косинус на пьедестале» для различных расширений символов. Отметим, что некоторый компромисс с точки зрения улучшения производительности и мощности обеспечивается в результате применения данных методов.

Если кодирование с коррекцией ошибок используют для уменьшения мощности несущего колебания, кодированные чипы потребуют более широкой полосы частот для поддержания заданной скорости передачи данных. Если скорость передачи данных r<1 ,то длительность чипа должна быть равна rТ_b и производительность системы с коррекцией ошибок равна

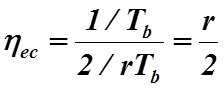.                                                                               (2.8.7)

Несмотря на то, что метод коррекции ошибок улучшает вероятность ошибки, производительность двухпозиционной фазовой манипуляции при этом ухудшается. Коррекция ошибок преднамеренно расширяет полосу частот, чтобы уменьшить требуемую мощность несущего колебания для заданной величины вероятности ошибок, которая противоположна желаемому улучшению производительности.

Производительность можно также улучшить, если не требуется выполнение условия постоянства огибающей. В этом случае мы можем увеличить число битов, закодированных в несущее колебание, позволив реализовать более двух амплитудных уровней, как в системе со сложной амплитудной манипуляцией. Если мы используем М уровней амплитуды, тогда log₂M бит можно закодировать в каждом пакете несущего колебания, обеспечив производительность согласно (2.8.5). Однако мощность несущего колебания (определяемая как среднее значение всех уровней амплитуды) должна быть увеличена, чтобы обеспечить существенное разделение М уровней для выполнения декодирования с требуемыми показателями (см. таблицу 2.4).  Точки для различных уровней при квадратурной амплитудной манипуляции представлены на рис. 2.28. Мы видим, что исключение условия о постоянной величине огибающей позволяет добиться улучшения производительности. К сожалению, несущие колебания с не постоянной амплитудой огибающей чувствительны к другим видам искажений в спутниковых линиях связи, что может воспрепятствовать улучшению производительности.

Теоретический анализ в области теории информации показал, что строгий верхний предел для производительности существует для любой системы связи. Данный предел производительности для аддитивного Гауссова шума определяется неравенством вида

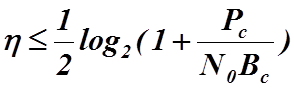.                                                                      (2.8.8)

Этот предел, отображенный на графике на рис. 2.29, показывает максимально возможное значение производительности для любого типа операций кодирования и декодирования. Мы видим, что практические методы кодирования в целом находятся ниже отмеченного предела. Однако другие попытки достижения максимально возможной производительности будут неизбежно сопровождаться более высокими уровнями обработки при декодировании и потребуют сложного оборудования при декодировании.