Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 2: "Модуляция, кодирование и декодирование", страница 4

Для двухпозиционной фазовой манипуляции используют фазовую модуляцию несущей вида (2.1.1в) модулирующим сигналом m(t):

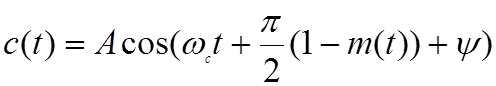.                                                      (2.3.6)

Данная модуляция дает бинарные фазовые сдвиги (0, π) на несущей частоте в соответствии с законом поступления импульсов модулирующего сигнала m(t). Используя тригонометрическую формулу , преобразуем выражение (2.3.6) к виду

.                                                              (2.3.7)

Амплитудный спектр несущей, модулированной с помощью двухпозиционной фазовой манипуляции, равен

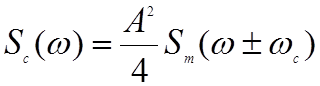.                                                                   (2.3.8)

Следовательно, амплитудный спектр несущей (2.3.8) получен простым смещением АМ спектра на величину несущей частоты.

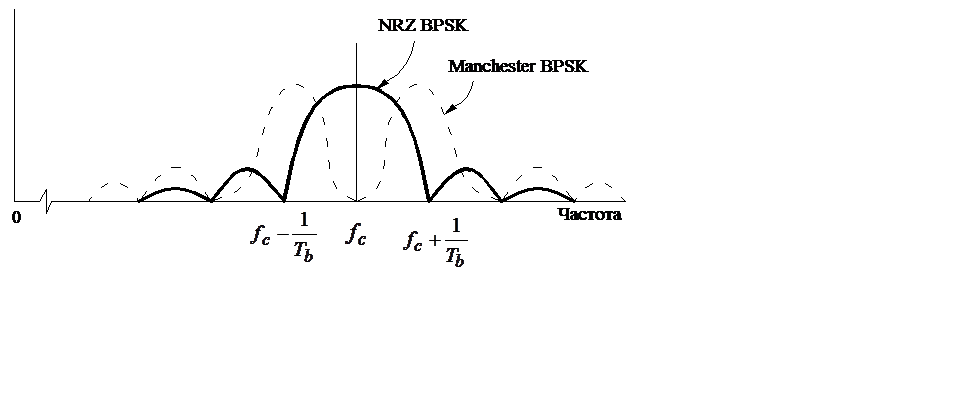Рис. 2.7. Спектры пилот-сигналов, модулированных с помощью двухпозиционной фазовой манипуляции.

Отметим, что для однополярных импульсов (NRZ) основная доля энергии спектра сосредоточена вблизи частоты f_c в пределах полосы частот 2/T_b , которая обычно используется в расчетах характеристик передаваемых сигналов, модулированных с помощью двухпозиционной фазовой манипуляции.

Так как величина 1/T_b определяет скорость передачи битов, то при двухпозиционной фазовой манипуляции требуется полоса в Герцах, равная приблизительно удвоенной скорости передачи данных в битах в секунду.

При модуляции пилот-сигнала двух полярными (Manchester) импульсами спектр несущей, симметричен относительно частоты f_c, имеет протяженность, равную 4/T_b ,которая в два раза шире спектра, занимаемого однополярными импульсами.

Мощность пилот-сигнала, модулированного с помощью двухпозиционной фазовой манипуляции равна P_c = A²/2 и одинакова для однополярных (NRZ) и двух полярных (Manchester) импульсов.

Квадратурная фазовая манипуляция (quadraturephaseshiftkeying - QPSK).

При квадратурной фазовой манипуляции (QPSK) последовательность информационных данных используют для одновременной двухпозиционной фазовой манипуляции квадратурных компонент одной и той же несущей.

На рис. 2. 8 представлен  принцип данного способа цифровой модуляции.

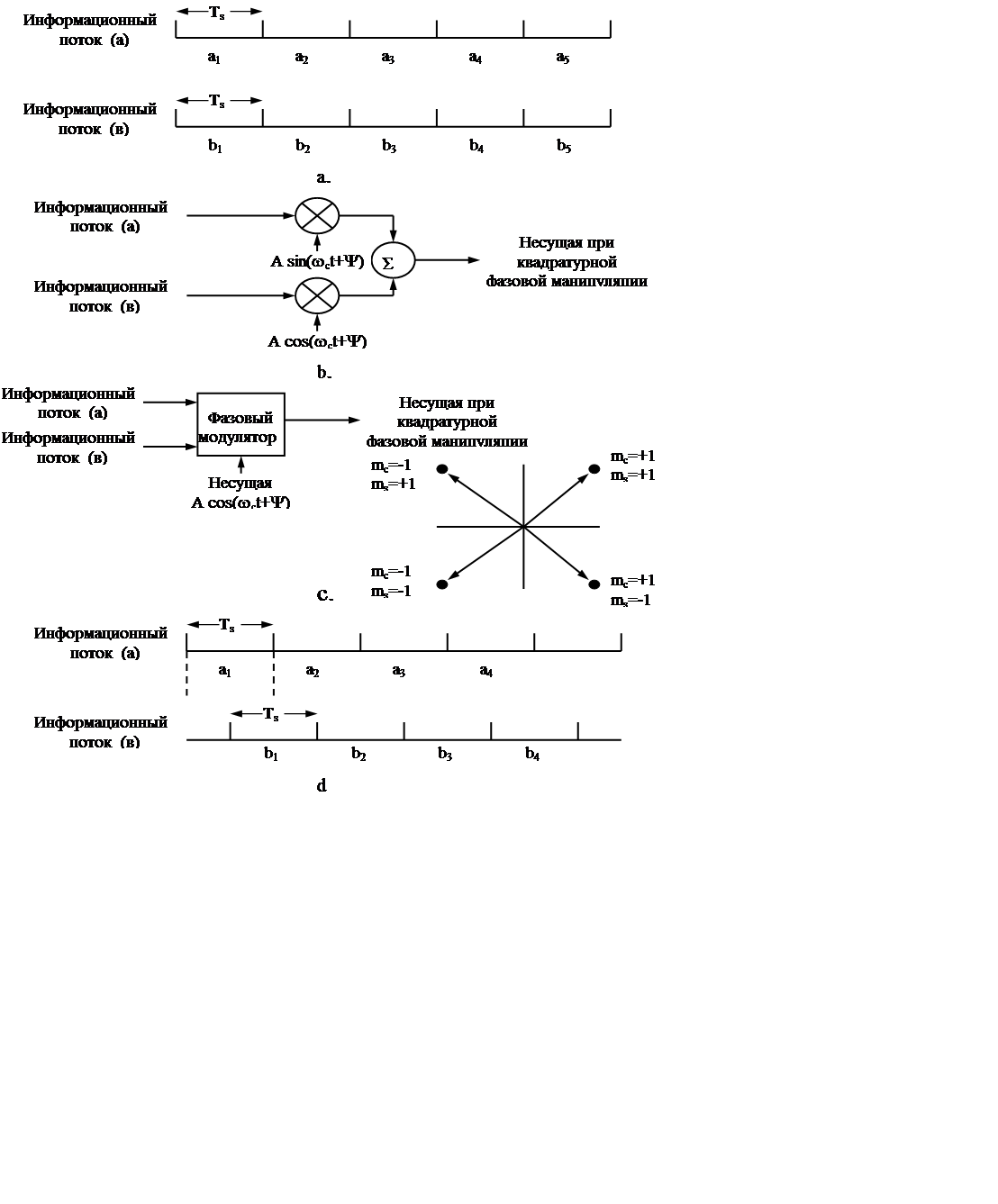
Рис.2.8. а) Синхронизация двух информационных потоков. b) Генератор пилот-сигнала с использованием квадратурной амплитудной модуляции. c) Генератор пилот-сигнала с использованием квадратурной фазовой манипуляции. d) Синхронизация двух информационных потоков при квадратурной фазовой манипуляции.

Два потока информации могут быть получены с выходов двух независимых источников цифровых данных или могут быть получены от одного источника. В каждый момент времени передается два бита. По этой причине интервалы времени следования квадратурных битов обозначены как T_s (такт символа), связанные с тактом следования битов на несущей T_b = T_s /2.

Пилот-сигнал в этом случае можно представить в виде выражения

,                         (2.3.9)

где m_c(t) и m_s(t) - обозначают модулирующие сигналы для каждой из двух последовательностей данных.

Последнее выражение соответствует АМ по двум квадратурным компонентам (косинусной и синусной) на одной и той же самой несущей.

После тригонометрических преобразований пилот-сигнал (2.3.9) можно представить в виде

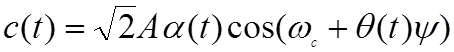,                                                  (2.3.10)

где ,                                                           (2.3.11а)

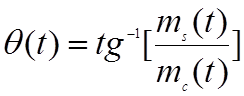.                                                                             (2.3.11б)

Фазовый угол в (2.3.11б) может принимать четыре значения (45, 135,

 -135 и - 45 градусов) в течение такта бита в зависимости от знака m_c(t) и m_s(t) . Следовательно, фазовый модулятор при квадратурной фазовой манипуляции (рис. 2. 8с) соответствует перескокам фазы несущей между этими угловыми значениями в зависимости от поступления битов из последовательностей m_c(t) и m_s(t) .

Из (2.3.10) следует, что мощность пилот-сигнала равна 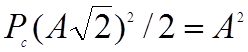, в то время как мощность каждой квадратурной компоненты равна А²/2 .

Спектр при квадратурной фазовой манипуляции равен

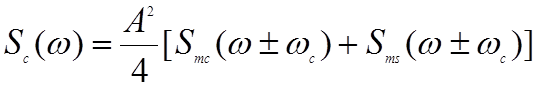.                                        (2.3.12)