Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 2: "Модуляция, кодирование и декодирование", страница 11

Вероятность ошибки в двоичном коде ограничена следующим пределом

,                                                                                   (2.6.4)

где r₀ - скорость среза для чипа (граничная скорость), равная

.                                                          (2.6.5)

Вероятность ошибки в двоичном коде, следовательно, можно оценить непосредственно по параметрам кода. Отметим, что поскольку скорость кодирования r меньше, чем скорость среза для чипа r₀ (последняя величина зависит от энергии чипа, и как следует из формул (2.6.5) и (2.6.2) вероятность ошибки в двоичном коде может быть уменьшена за счет увеличения длины блока чипа n (и, следовательно, за счет увеличения длины блока данных k, так как k=rn). Это просто подтверждает тот факт, что для фиксированной скорости кодирования k/n, чем больше величины k и n , тем больше  разность k-n и тем больше ошибок в двоичном коде может быть допущено. Количество вычислительных процедур, необходимое для преобразования декодированных чипов в декодированные биты, возрастает по закону 2^к.

Рис. 2. 22. Зависимость вероятностей ошибок в двоичном коде от длины кода блока k и от r /r₀  (r скорость кодирования=k/n; r₀ - скорость среза в канале связи).

Следовательно, сложность декодирования и требуемое время обработки резко увеличиваются при увеличении длины блока коррекции ошибок.

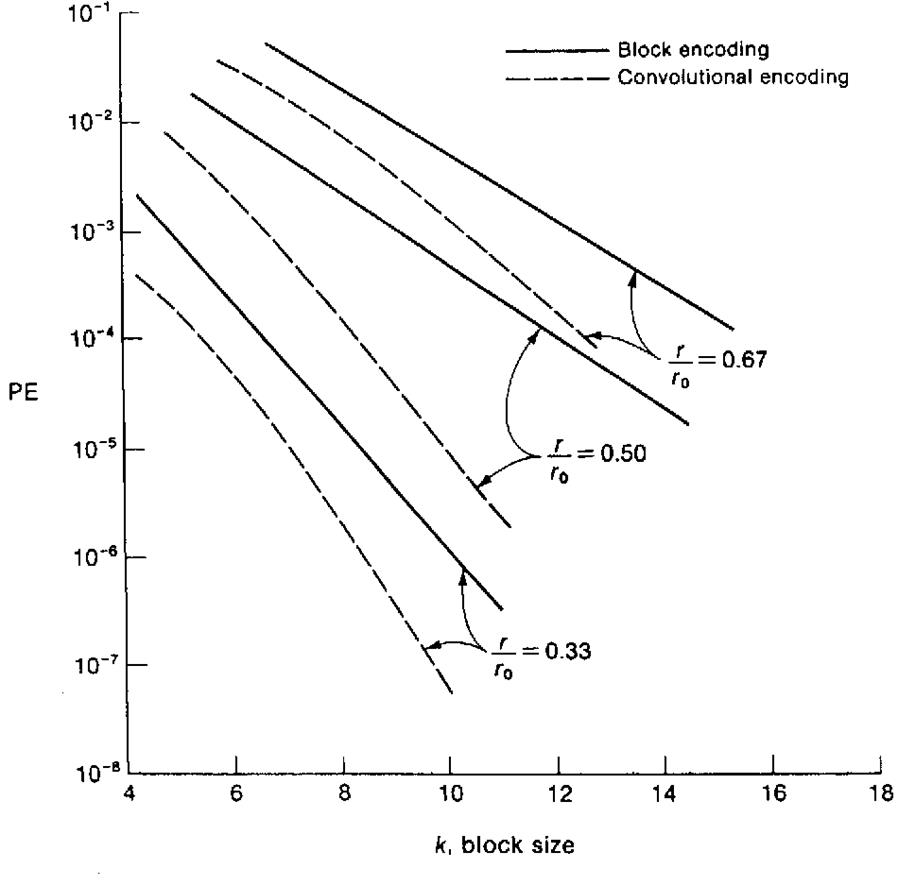
На рис. 2.22 представлены графики зависимостей пределов вероятностей ошибки в двоичном коде как функций длины кода блока kдля разных значений r /r₀ . Обычно, величина ε≤10^-3 , для которой r₀ в выражении (2. 6. 5) равно приблизительно 1, а отношение r /r₀ равно приблизительно скорости кодирования r согласно формулы (2.6.1).

Улучшение вероятности ошибок в двоичном коде может быть достигнуто за счет усложнения метода кодирования. Однако, как уже отмечалось выше, при этом количество вычислительных процедур резко возрастает с ростом k.

Кодирование на основе процедуры свертки.

Сверточное кодирование – это метод кодирования битов данных в передаваемые чипы, при котором последующее декодирование чипов обеспечивает улучшение декодирования битов. Процесс декодирования достигается обнаружением одного бита одновременно в последовательности данных с помощью скользящих последовательностей принимаемых чипов. Оптимальное декодирование выполняют с помощью алгоритма декодирования Витерби, который позволяет «извлекать» биты из декодированных чипов.

Процедура свертки  при сверточном кодировании порождает коды, которые могут быть декодированы с лучшими показателями по вероятностям ошибок в двоичных кодах по сравнению с обычным блочным кодированием при одинаковой скорости и длине блока. Поскольку сверточные кодеры не более сложны, чем блочные кодеры, сверточное кодирование представляется более перспективным для коррекции ошибок. Анализ точности представляется более трудным вследствие чередующегося характера кодируемых битов. Для скорости кодирования r и постоянной длины k (количество предыдущих битов, присутствующих после свертки в каждом чипе), существует  сверточный код  с вероятностью  ошибки в двоичном коде, подчиняющейся следующему условию

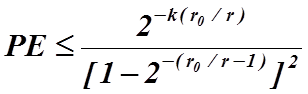.                                                            (2.6.6)

Из рис. 2.22 следует вывод о преимуществе  сверточных кодов по сравнению с кодами фиксированной длины.

Сверточное декодирование может  быть улучшено с помощью так называемых алгоритмов «мягкого решения», которые обеспечивают улучшение скорости среза до значения

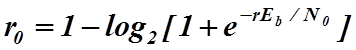                                                       (2.6.7)

по сравнению с величиной, определенной формулой (2.6.5).

Данный алгоритм дает те же значения r₀ ,что и (2.6.5) при значении Е_b , меньшем на 2 дБ. Следовательно, при определении вероятности ошибок в двойном коде по графикам на рис. 2.22 при фиксированных значениях k и r /r₀ , можно обеспечить показатели с энергией Е_b , меньшей на 2 дБ. Однако рассматриваемый алгоритм требует использования более сложного декодера.

Как сверточные, так и блочные коды, в которых выполняется процедура коррекции ошибок, улучшают вероятность ошибок в двоичном коде.