Второй способ, исключающий применение когерентного опорного сигнала, связан с использованием частотной манипуляции (FSK) (см. формулу (2. 3. 14)). Так как модуляция по битам содержится в несущем колебании, то бит может быть декодирован с помощью измерения частоты принятого несущего колебания. Данные частотные измерения могут быть проведены без знания фазы. При бинарной частотной манипуляции процесс декодирования сопровождается фильтрацией с помощью перестраиваемых полосовых фильтров, настроенных на каждую из модулирующих частот и оценкой энергии в течение длительности бита для определения того, какой из фильтров выделяет максимальную энергию (рис. 2. 20б). Если частоты разнесены достаточно далеко, то только один из фильтров будет содержать энергию несущего колебания, а на выходе второго фильтра будет присутствовать шум.
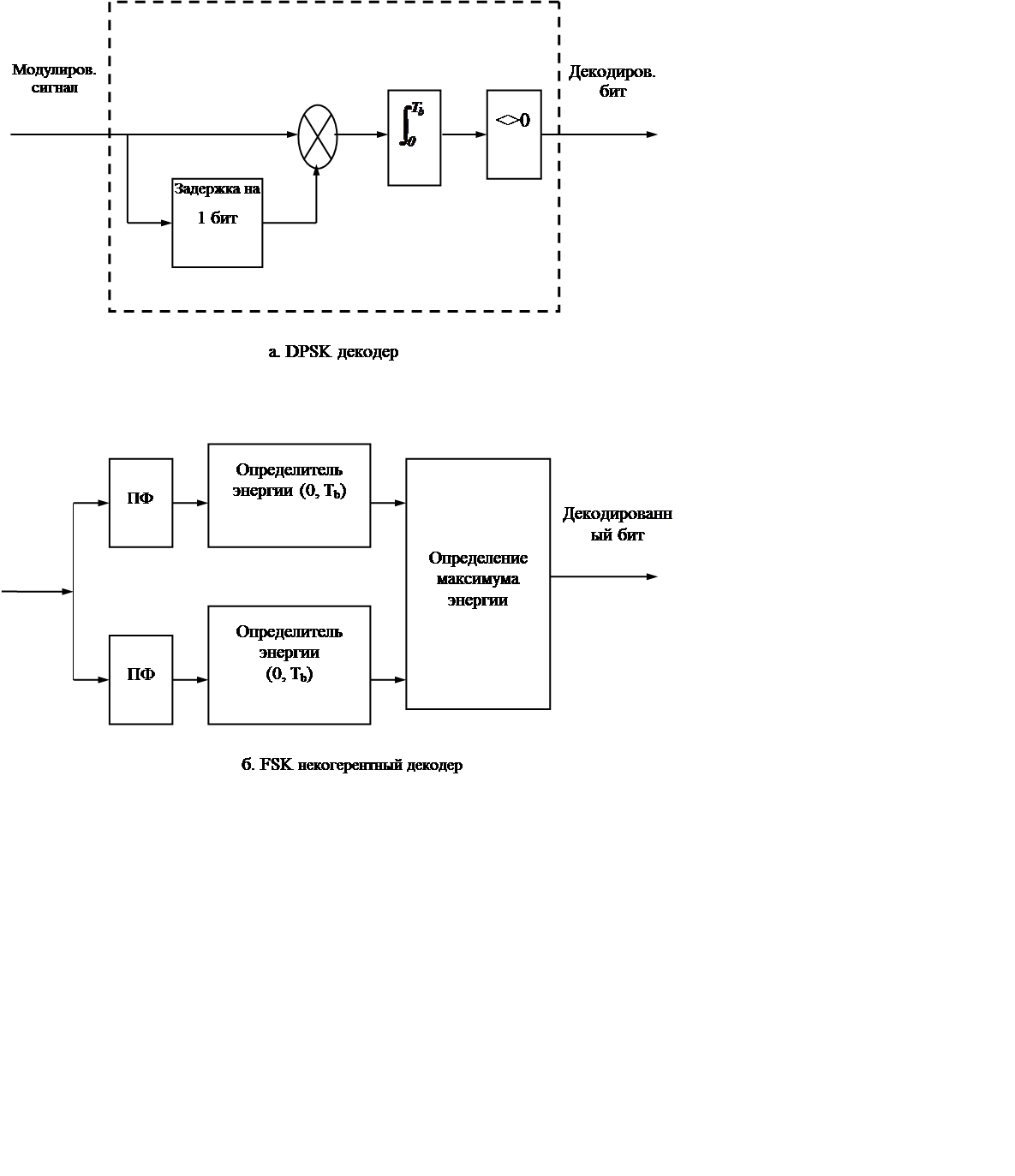
Рис. 2. 20. а) DPSK декодер. б) FSK декодер.
Результирующие вероятности ошибок в двоичных разрядах приведены в
Таблице 2. 3 и на рис. 2. 17. Отметим, что этот вид некогерентного частотного декодирования также дает худшие (большие значения) показатели по вероятностям ошибок в двоичных разрядах по сравнению со случаем когерентной двухпозиционной фазовой манипуляции со смещением (BPSK) при одинаковых величинах энергии. Частотная манипуляция (FSK) приблизительно на 4 дБ хуже при вероятности ошибки = 10-3 и на 3 дБ хуже при вероятности ошибки = 10-5.
Сигналы с частотной манипуляцией (FSK) можно также выявлять с помощью частотной демодуляции несущего колебания для восстановления полосы частот модулирующего m(t) сигнала, а затем с помощью интегрирования и определения знака в течение длительности бита для определения битов, содержащихся в m(t). Такая система хуже на 1 дБ по сравнению с декодером, выполняющим обнаружение сигнала с помощью полосовых фильтров, как показано на рис. 2. 17.
2. 6. Кодирование с исправлением ошибок
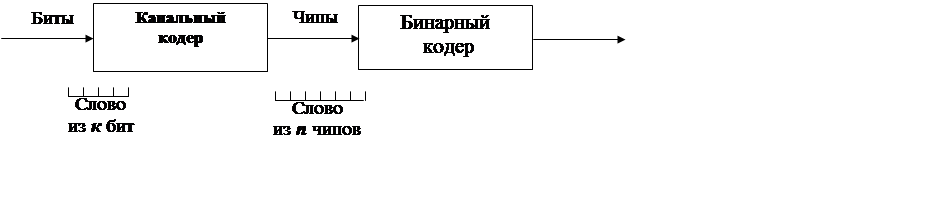
При блочном кодировании с исправлением (коррекцией) ошибок каждый блок из к битов вначале кодируют (отображают) в определенных блоках (n > к) канальных битов (называемых канальными символами или бодами, или чипами), как показано на рис. 2. 21.
 |
Скорость кодирования при этом равна
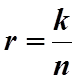. (2.6.1)
Каждый последующий блок данных из к битов данных преобразуют в блок из n чипов в соответствии с предписанным законом кодирования. Затем чипы посылают по бинарному каналу в виде битов данных. Если n чипов декодированы правильно, то к бит данных, которым они соответствуют, немедленно будут идентифицированы и биты данных будут переданы правильно. Если некоторые из n чипов декодированы неправильно, однако, к битов данных все еще могут быть правильно обнаружены, то «экстра» чипы используют для представления к битов. Некоторые чипы в блоке могут быть декодированы неправильно без неправильного декодирования битов данных в блоке. Если это имеет место, результирующая вероятность ошибки будет меньше, чем вероятность ошибки чипа для той же мощности колебаний несущей чипа. Количество чипов, которые могут содержать ошибки, перед тем, как ошибка в данных имеет место, связано с законом кодирования, который отображает к битов в n чипах.
Вероятность ошибки (см. Таблицу 2. 4), при которой переданный чип будет декодирован с ошибкой при использовании методов фазового когерентного кодирования, равна
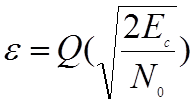, (2.6.2)
где Ес – это энергия в расчете на один чип. Если скорость посылаемых битов фиксирована, то скорость чипов может быть выше, чем эта скорость (вследствие более короткой временной длительности чипа, однако при более широкой полосе частот пилот-сигнала), может быть передано большее количество чипов. Это означает, что временной интервал, отведенный для передачи чипа, меньше временного интервала, отведенного для передачи бита, т. е.
(2.6.3)
где - r скорость кодирования (см. 2. 6. 1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.