Однако в манипуляторе часто можно выделить основной механизме несколькими степенями свободы и, пренебрегая звеньями приводных механизмов, говорить о наличии незамкнутой кинематической цепи. Этот основной механизм отражает основные кинематические и динамические свойства манипулятора как системы с несколькими степенями свободы.
Число степеней свободы манипулятора равно числу обобщенных координат, под которыми понимают независимые переменные, однозначно определяющие положение манипулятора в пространстве.
Кинематические пары накладывают ограничения, как на относительное, так и на абсолютное движение звеньев. Связи могут накладываться на манипулятор также в процессе выполнения рабочих операций.
Связи могут быть выражены уравнениями или неравенствами, связывающими координаты и их производные по времени. Связи называются кинематическими или дифференциальными, если они устанавливают связь между координатами и их производными по времени. Если уравнение дифференциальной связи может быть проинтегрировано, то оно сводится к зависимости только между координатами, такая связь называется геометрической или голономной.
Голономные связи выражаются уравнениями вида
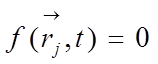 ,
,
где 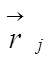 —
радиус-вектор произвольной j-й точки системы;
—
радиус-вектор произвольной j-й точки системы;
t — время.
Если уравнение дифференциальной связи не может быть проинтегрировано» то такая связь называется неголономной.
Неголономные связи выражаются дифференциальными уравнениями вида
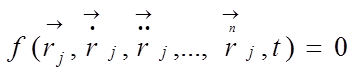 ,
,
где число точек над вектором означает порядок производной по времени.
Для манипуляторов (так как они являются управляемыми системами) следует выделить программные связи, которые выражают условия, накладываемые на движения манипуляторов в процессе выполнения ими рабочих операций. Будем считать, что условия движения манипулятора могут быть выражены уравнениями и неравенствами, так же как и связи.
Принципиальное отличие программных связей от обычных связей механических неуправляемых систем состоит в том, что первые реализуются с помощью управляющих сил, и вторые реализуются, как правило, геометрически и имеют место во все время движения.
Следует отметить, что для реализации программных |язей манипулятором в его приводах должны быть приложены дополнительные силы, которые можно назвать реакциями программных связей.
Реакциями связей называют силы, приложенные к механической системе со стороны других тел, а также силы действия звеньев друг на друга в кинематических парах манипулятора. Число составляющих реакций в кинематических парах равно классу кинематической пары.
Для автоматизированного кинематического и динамического анализа механизмов на ЭВМ необходимо кодирование параметров, описывающих структуру, геометрию и распределение масс системы.
Для описания структуры манипуляторов весьма удобным и универсальным является метод графов, основанный на понятии структуры дерева. При этом важное значение имеет понятие пути между двумя телами. Под путем между двумя телами понимается совокупность векторов, проходящих через шарниры кинематической цепи, соединяющей тела, при котором ни один шарнир не проходится дважды.
Тогда структуру типа дерева можно определить как структуру, для которой между всеми парами тел путь определяется единственным образом. Очевидно, что кинематические цепи со структурой типа дерева являются незамкнутыми кинематическими цепями. Такие структуры могут быть приведены к замкнутым путем добавления уравнений связей. Если существуют два различных пути между двумя телами, то система содержит замкнутую кинематическую цепь.
П. Б. Слиеде был предложен алгоритм кодирования механических систем со структурой дерева методом графов. Этот метод удобен тем, что любой механизм с замкнутыми и разомкнутыми кинематическими цепями можно свести к структуре типа дерева с дополнительными геометрическими связями. Для таких структур просто выбираются обобщенные координаты и легко записываются уравнения связей. Поэтому такие структуры получили широкое распространение в динамике систем твердых тел.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.