Введение в робототехнику. Цикловое управление манипуляторами и технологическим оборудованием, страница 12

Рабочий орган, закрепленный на конечном звене ма­нипулятора, в "процессе его перемещения по заданной траектории при выполнении какой-либо технологической операции должен быть определенным образом сориенти­рован. Так, сварочная головка для обеспечения качества тарного шва должна в любой момент находиться под определенным углом к стыку свариваемых деталей. Ориентация рабочего органа в пространстве обеспечивается с помощью ориентирующих степеней подвижности мани­пулятора. Ориентирующие движения называются также локальными.

Кинематические характеристики исполнительной части робота зависят от числа степеней подвижности, их пила и сочетания. Именно эти особенности кинематиче­ской схемы робота выражаются понятием системы коор­динат, в которой работает робот.

Как известно, положение точки в пространстве определяется тремя ее координатами, причем в различных системах координат ее координаты различны. В робототехнике различают четыре такие системы: декартова (прямоугольная), цилиндрическая, полярная и угловая. Разберем особенности каждой из них.

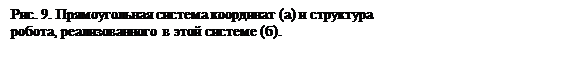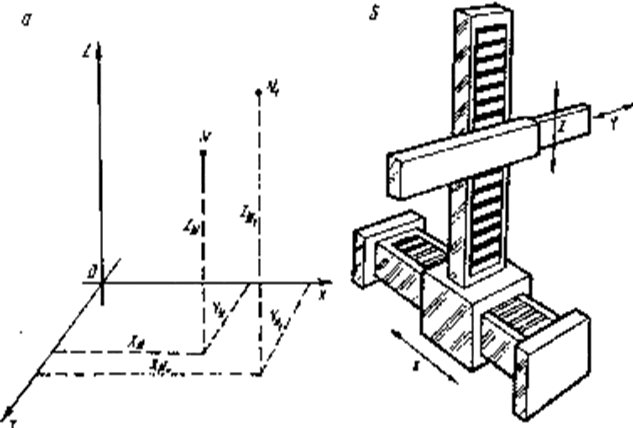
Предположим, что в пространстве задана точка N (рис. 9). Ее положение однозначно может быть задано тремя координатами — X_N , Y_N , Z_N . При перемещении этой точки в пространстве в положение N₁ изменятся и ее координаты: они станут равными X_N1 , Y_N1 , Z_N1 . Величи­ны приращения (т. е. перемещения) по всем координа­там составят: ∆X=X_N1 – X_N ; ∆Y=Y_N1 – Y_N ;

∆Z=Z_N1 – Z_{N .}

Следовательно, задача перемещения в пространстве определенной точки, например конца охвата манипуля­тора, работающего в прямоугольной системе координат, сводится к перемещению ее по каждой координате в отдельности.

Положение точки в цилиндрической системе коорди­нат (рис. 10) также задается тремя величинами: радиусом, параллельным одной из плоскостей (на нашем рисунке плоскости XOY) прямоугольной системы координат высотой смещения Н этого радиуса от параллельному (базовой) плоскости и углом поворота j этого радиуса r относительно другой базовой плоскости отсчета (в  нашем случае ZOX).

Пусть за некоторое время точка N переместилась в положение N­­­1. Тогда ее положение будут характеризовать новые значения параметров: rN1 , HN1 , jN1 ; их приращения: ∆r=r­N1 – rN ; ∆H= HN1 – HN ; ∆j= jN1 - jN .

Если представить, что длина руки манипулятора соответствует величине радиуса r, то для достижения за­данной точки в пространстве манипулятор должен поднять руку на высоту этой точки, выдвинуть руку на величину, равную радиусу r, и развернуть ее на угол j.

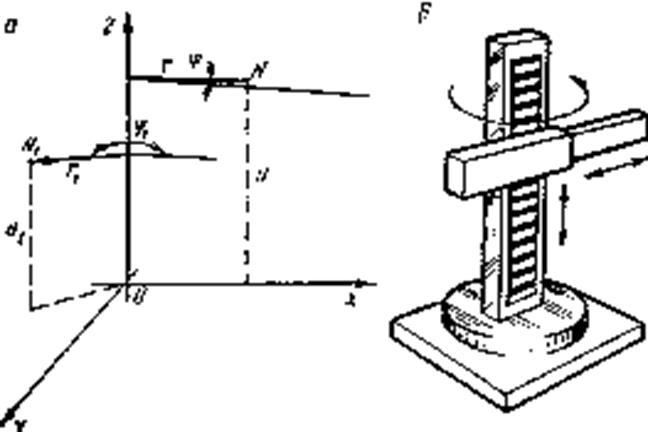
В сферической (полярной) системе координат (рис. 11) положение точки в пространстве также задается тремя параметрами: радиусом, на котором точка N расположе­на относительно выбранного полюса р; углами a и b на­клона радиуса r относительно двух базовых взаимно перпендикулярных плоскостей К и М, причем полюс р принадлежит обеим плоскостям.

Очевидно, что при изменении положения точки N в пространстве изменятся и все параметры, определяющие ее положение. Их приращения будут иметь вид:  ∆r=rN1 - rN ; ∆a=aN1 - aN ; ∆b=bN1 - bN .

Достаточно установить руку манипулятора, действую­щего в полярной системе координат, под углами a и b и выдвинуть ее на величину r, и тем самым будет до­стигнута нужная точка пространства.

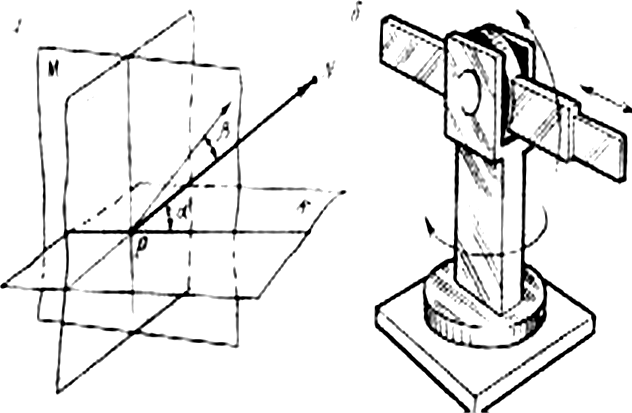
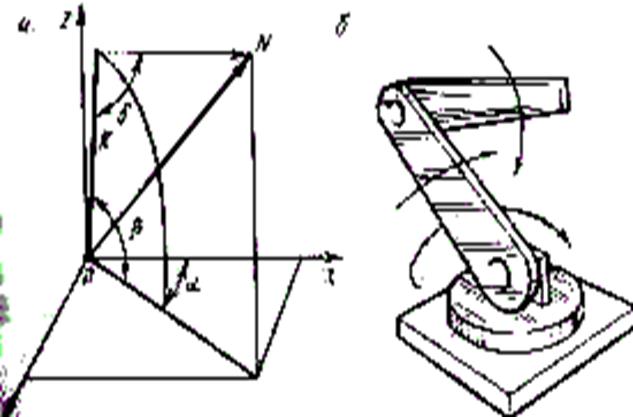
В угловой системе координат (рис. 12) положение точки в пространстве задано тремя углами a, b, g, при­чем углы b и g лежат в одной плоскости. Тем самым при определенном соотношении длин звеньев может быть до­стигнута любая точка рабочей зоны. Перемещение же от точки к точке будет задано как изменение всех трех уг­лов:  ∆a=aN1 - aN ; ∆b=bN1 - bN ; ∆g=gN1 - gN .

Манипуляторы, действующие в угловой системе координат, называются еще антропоморфными (человекоподобными), так как они более всего напоминают руку человека.

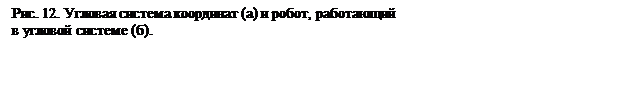На рис. 9—12 приведенные для различных систем координат зависимости показывают, каким образом рабочий орган, закрепленный на конечном звене манипулятора, может быть перемещен в любую точку в пределах рабочей зоны робота.