















5. Электростатика проводников. Основные закономерности электростатических полей.Свойства электростатического поля Электростатическое поле проводников, расположенных, в диэлектрике. Электростатическая индукция. Электрическая емкость проводника. Электростатическая энергия проводников. Теорема Ирншоу. Электрический диполь и квадруполь. Методы решения электростатических задач (методы: изображений, инверсии, разделения переменных, конформного отображения). Сведение объемных сил в электростатике к поверхностным натяжениям. Тензор натяжения.
5.1. Свойства электростатического поля. Электростатическое поле проводников, расположенных в диэлектрике. Предмет макроскопической электродинамики составляет изучение электромагнитных полей в пространстве, заполненным веществом. Вид уравнений Максвелла. (четыре формы записи уравнений) зависит от физической природы материальной среды. По этой причине целесообразно производить исследования для каждой категории физических объектов в отдельности. В отношении электрических свойств все среды делятся на две категории: проводники и изоляторы (диэлектрики). Первые отличаются от вторых тем, что электрическое поле вызывает в них направленное движение свободных зарядов – электрический ток проводимости. Не слишком сильные электрические поля не вызывают ток в диэлектрике. В сильных электрических полях возникает электрический ток и даже возможен пробой диэлектрика. На первом этапе изучим те свойства проводников и диэлектриков, которые не зависят от деталей их структуры. При этом ограничимся рассмотрением полей малой амплитуды в линейном приближении.
Сначала рассмотрим основные следствия, вытекающие из уравнений Максвелла в электростатической ситуации, когда заряды неподвижны. Токи отсутствуют
![]() ,
,
![]() .
.
Эта система
уравнений не замкнута, она содержит, две векторные неизвестные функции ![]() и одну скалярную
и одну скалярную ![]() .
Для описания электростатических задач в конкретных средах необходимо добавить
материальные соотношения
.
Для описания электростатических задач в конкретных средах необходимо добавить
материальные соотношения ![]() . При наличии границ
раздела сред еще нужно добавить граничные условия
. При наличии границ
раздела сред еще нужно добавить граничные условия
![]()
Из условия неподвижности зарядов и отсутствия токов следует отсутствие магнитного поля и поля магнитной индукции.
Следствием
уравнения ![]() является отсутствие циркуляции, поле
является отсутствие циркуляции, поле ![]() потенциально
потенциально
![]()
и поле ![]() перпендикулярно эквипотенциальным поверхностям
перпендикулярно эквипотенциальным поверхностям
![]() , так как вектор
, так как вектор ![]() ортогонален
поверхностям
ортогонален
поверхностям ![]() .
.
Не трудно
убедиться, что работа ![]() электростатической силы по
перемещению единичного заряда из точки
электростатической силы по
перемещению единичного заряда из точки ![]() в точку
в точку
![]() не зависит от пути перемещения
не зависит от пути перемещения ![]() , а определяется только положением точек
, а определяется только положением точек ![]() и
и ![]()
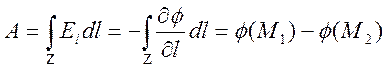 .
.
В случае замкнутого
контура ![]() и работа
и работа ![]() равна
нулю.
равна
нулю.
Рассмотрим основные положения, вытекающие из электростатики, применительно к заряженным проводникам, расположенным в идеальном диэлектрике, в котором нет свободных зарядов.
1. Напряженность электрического поля внутри проводника
должна равняться нулю, так как отличное от нуля электрическое поле ![]() привело бы к возникновению тока в этом
проводнике. Протекание же тока в проводнике связано с диссипацией энергии и
потому не может само по себе (без сторонних источников) поддерживаться в
стационарном состоянии, значит
привело бы к возникновению тока в этом
проводнике. Протекание же тока в проводнике связано с диссипацией энергии и
потому не может само по себе (без сторонних источников) поддерживаться в
стационарном состоянии, значит ![]() . Из условия
. Из условия ![]() следует, что
следует, что ![]() внутри
проводника и на его поверхности. По этой причине поверхность проводника
эквипотенциальна.
внутри
проводника и на его поверхности. По этой причине поверхность проводника
эквипотенциальна.
2. Следствием того, что в состоянии равновесия электрическое поле внутри
проводника равно нулю, является отсутствие объемных зарядов в проводнике ![]() . Действительно, если в толще проводника
провести произвольную замкнутую поверхность, то на этой поверхности электрическое
поле равно нулю, равен нулю и поток напряженности поля через эту поверхность.
Согласно теореме Гаусса, следует отсутствие зарядов внутри такой произвольной
замкнутой поверхности. Все заряды в проводнике вытесняются на его поверхность и
распределены там таким образом, чтобы, создаваемые ими внутри проводника поля
взаимно компенсировались.
. Действительно, если в толще проводника
провести произвольную замкнутую поверхность, то на этой поверхности электрическое
поле равно нулю, равен нулю и поток напряженности поля через эту поверхность.
Согласно теореме Гаусса, следует отсутствие зарядов внутри такой произвольной
замкнутой поверхности. Все заряды в проводнике вытесняются на его поверхность и
распределены там таким образом, чтобы, создаваемые ими внутри проводника поля
взаимно компенсировались.
3. Таким образом, задача электростатики проводников сводится к определению электрического поля в диэлектрике, вне проводников, и к определению распределения зарядов по поверхности проводников.
4. Согласно граничному условию тангенциальная
компонента вектора электрического поля непрерывна при переходе через границу
раздела сред. В проводнике ![]() , значит тангенциальная
компонента
, значит тангенциальная
компонента ![]() вектора электрического поля на поверхности
проводника равна нулю. В противном случае происходило бы непрерывное движение
зарядов вдоль поверхности, а это невозможно из за наличия потерь и это
противоречит понятию электростатики (отсутствие токов). Таким образом, вне
проводника вблизи его поверхности электрическое поле направлено нормально к
поверхности проводника. Этот вывод согласуется с ортогональностью
электрического поля эквипотенциальным поверхностям (поверхность проводника
эквипотенциальна).
вектора электрического поля на поверхности
проводника равна нулю. В противном случае происходило бы непрерывное движение
зарядов вдоль поверхности, а это невозможно из за наличия потерь и это
противоречит понятию электростатики (отсутствие токов). Таким образом, вне
проводника вблизи его поверхности электрическое поле направлено нормально к
поверхности проводника. Этот вывод согласуется с ортогональностью
электрического поля эквипотенциальным поверхностям (поверхность проводника
эквипотенциальна).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.