Задача
типа Б). На изолированном шаре помещен заряд ![]() .
.
Рассмотрим сначала случай задания на поверхности
шара граничного условия ![]() и найдем положение и
величину мнимого заряда (изображения)
и найдем положение и
величину мнимого заряда (изображения) ![]() , при
котором обеспечивалось бы выполнение этого граничного условия в отсутствие
проводящего шара. Сначала выберем точку
, при
котором обеспечивалось бы выполнение этого граничного условия в отсутствие
проводящего шара. Сначала выберем точку ![]() на
поверхности шара
на
поверхности шара ![]() . Расстояние от зарядов
. Расстояние от зарядов ![]() и
и ![]() до
поверхности шара обозначим через
до
поверхности шара обозначим через ![]() и
и ![]() . На этой поверхности должно выполняться
условие
. На этой поверхности должно выполняться
условие ![]() :
:
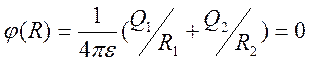 ,
, ![]() ,
,
из которого следуют соотношения
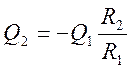 ,
, 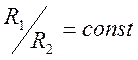 (5.9)
(5.9)
Здесь ![]() - диэлектрическая
проницаемость среды вне шара,
- диэлектрическая
проницаемость среды вне шара, ![]() - расстояния зарядов
- расстояния зарядов ![]() до точек на поверхности
до точек на поверхности ![]() , смысл обозначений
, смысл обозначений ![]() понятен
из Рис.5.5. Из формулы (5.9) видно, что знак изображения («зеркального») заряда
противоположен знаку
понятен
из Рис.5.5. Из формулы (5.9) видно, что знак изображения («зеркального») заряда
противоположен знаку ![]() и величина отношения
и величина отношения 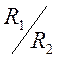 не зависит от положения точки на
поверхности шара. Заряд
не зависит от положения точки на
поверхности шара. Заряд ![]() должен находиться
внутри шара на линии, соединяющей центр шара с зарядом
должен находиться
внутри шара на линии, соединяющей центр шара с зарядом ![]() .
Найдем теперь положение заряда
.
Найдем теперь положение заряда ![]() . С этой целью выберем
положение точки
. С этой целью выберем
положение точки ![]() , как показано на Рис. 5.6. Тогда
для точки
, как показано на Рис. 5.6. Тогда
для точки ![]() имеем:
имеем: ![]() ,
, ![]() ,
, 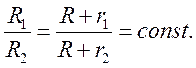
Для точки ![]() имеем
имеем ![]() ,
, ![]() ,
, 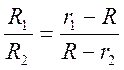 .
.
Так как потенциал в точках ![]() и
и ![]() одинаков (в данной задаче он равен нулю),
то
одинаков (в данной задаче он равен нулю),
то
приравнивая полученные для точек ![]() и
и ![]() отношения
отношения 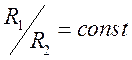 ,
получим положение заряда – изображения
,
получим положение заряда – изображения 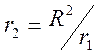 и
величину
и
величину 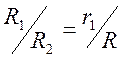 . Величина заряда
. Величина заряда ![]() представляется
в виде
представляется
в виде
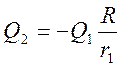 .
.
Найденный фиктивный заряд ![]() в совокупности с
зарядом
в совокупности с
зарядом ![]() обеспечивает выполнение граничного условия
обеспечивает выполнение граничного условия
![]() . Следовательно, в произвольной точке
потенциал имеет представление
. Следовательно, в произвольной точке
потенциал имеет представление
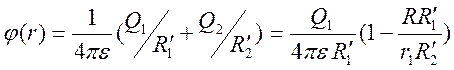 ,
,
которое дает решение рассматриваемой задачи, смысл расстояний ![]() ясен из Рис. 5.5.
ясен из Рис. 5.5.
Если на поверхности сферы ![]() задано
условие
задано
условие ![]() , то для выполнения этого условия в центр
шара необходимо поместить дополнительный фиктивный точечный заряд
, то для выполнения этого условия в центр
шара необходимо поместить дополнительный фиктивный точечный заряд ![]() . Решение такой задачи выразится суммой
потенциалов от трех точечных зарядов (одного реального и двух фиктивных)
. Решение такой задачи выразится суммой
потенциалов от трех точечных зарядов (одного реального и двух фиктивных)
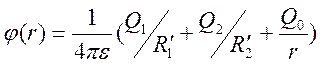 .
.
Задача типа Б). На
проводящем шаре задан полный заряд ![]() . Сначала исследуем
случай разряженного шара:
. Сначала исследуем
случай разряженного шара: ![]() на поверхности шара. Решение
такой задачи сконструируем из решения для случая
на поверхности шара. Решение
такой задачи сконструируем из решения для случая ![]() . Чтобы
удовлетворить условию
. Чтобы
удовлетворить условию ![]() , добавим к заряду
, добавим к заряду ![]() еще один фиктивный заряд
еще один фиктивный заряд ![]() , поместив его в центр шара. При этом полный
заряд на поверхности шара равен нулю. Тогда решение для потенциала вне шара
примет вид
, поместив его в центр шара. При этом полный
заряд на поверхности шара равен нулю. Тогда решение для потенциала вне шара
примет вид
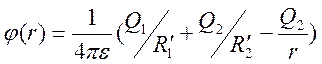 .
.
Если на поверхности шара задан полный заряд ![]() , то тогда в центр шара поместим фиктивный
заряд
, то тогда в центр шара поместим фиктивный
заряд ![]() , это обеспечит выполнение условия
, это обеспечит выполнение условия ![]() . Решение этой задачи имеет вид
. Решение этой задачи имеет вид
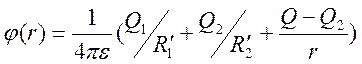 .
.
Отметим в заключение, что метод изображений имеет ограниченную область применения, так как в случае сложных форм проводников нахождение изображения зарядов оказывается весьма трудной задачей. Но при простых границах проводников этот метод позволяет быстро получать решения, имеющие к тому же простой физический смысл.
Метод инверсии. Это простой метод, который позволяет по известному решению одной электростатической задачи находить решение другой задачи. Основанием этого метода является инвариантность уравнения Лапласа к определенному преобразованию переменных (преобразование инверсии). Например, в сферических координатах уравнение Лапласа имеет вид
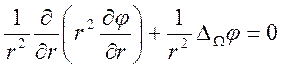 ,
,
где
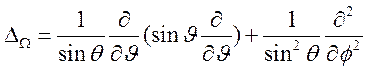 - угловая часть оператора Лапласа. Это
уравнение сохраняет свою форму, если вместо переменной
- угловая часть оператора Лапласа. Это
уравнение сохраняет свою форму, если вместо переменной ![]() ввести
новую переменную
ввести
новую переменную ![]() , такую, что имеет место
пропорциональность
, такую, что имеет место
пропорциональность ![]() :
:
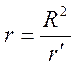 ,
, 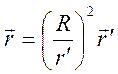 ,
,
где
![]() - радиус инверсии
- радиус инверсии
Одновременно делается заменуа неизвестной функции
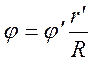 .
.
Такое
преобразование меняет фигуры всех протяженных проводников и их взаимное
расположение. Меняются величины и расположение всех точечных зарядов. Граничное
условие ![]() на поверхности проводника автоматически
выполняется новым решением
на поверхности проводника автоматически
выполняется новым решением ![]() . Таким образом, по
известному решению
. Таким образом, по
известному решению ![]() находится еще новое решение
находится еще новое решение
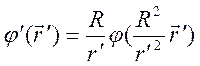 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.