Электростатическое поле в вакууме вне источников удовлетворяет двум однородным уравнениям
![]() .
.
Первое уравнение позволяет ввести скалярный потенциал
![]() ,
,
а второе уравнение указывает на существование векторного потенциала
![]() .
.
Введем систему координат так, что
![]() . Тогда
. Тогда ![]() можно
выбрать однокомпонентным вектором
можно
выбрать однокомпонентным вектором ![]() и компоненты поля имеют
представление
и компоненты поля имеют
представление
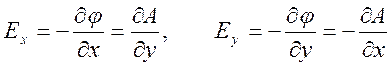 .
.
Такие соотношения между функциями
![]() и
и ![]() совпадают
с условиями Коши – Римана, выражающими тот факт, что комплексная функция
совпадают
с условиями Коши – Римана, выражающими тот факт, что комплексная функция
![]() ,
,
является аналитической функцией
комплексного аргумента ![]() .
. ![]() называется комплексным потенциалом.
Факт аналитичности означает, что функция
называется комплексным потенциалом.
Факт аналитичности означает, что функция ![]() в
каждой точке имеет производную, не зависящую от направления, в котором она
берется. В частности, дифференцируя вдоль направления оси
в
каждой точке имеет производную, не зависящую от направления, в котором она
берется. В частности, дифференцируя вдоль направления оси ![]() , получим
, получим
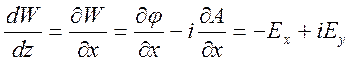 .
.
Силовые линии поля описываются уравнением
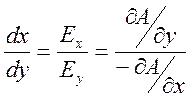 .
.
Это можно представить в форме 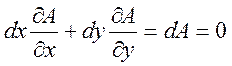 .
.
Значит ![]() и
силовые линии поля
и
силовые линии поля ![]() это линии
это линии ![]() . Эквипотенциальные поверхности
. Эквипотенциальные поверхности ![]() - это линии
- это линии ![]() .
Функциональное соотношение
.
Функциональное соотношение ![]() осуществляет конформное
отображение комплексного переменного
осуществляет конформное
отображение комплексного переменного ![]() на
плоскость комплексного переменного
на
плоскость комплексного переменного ![]() . Пусть требуется найти
электростатическое поле проводящего тела. Сечение этого проводника в плоскости
. Пусть требуется найти
электростатическое поле проводящего тела. Сечение этого проводника в плоскости ![]() обозначим
обозначим ![]() и пусть
известно значение потенциала на этом контуре
и пусть
известно значение потенциала на этом контуре ![]() .
Найдем функцию
.
Найдем функцию ![]() , осуществляющую отображение
контура
, осуществляющую отображение
контура ![]() с плоскости
с плоскости ![]() на
линию
на
линию ![]() параллельную оси ординат в плоскости
параллельную оси ординат в плоскости ![]() . Такая функция
. Такая функция ![]() дает
значение потенциала
дает
значение потенциала ![]() . Способ отыскания конформного
отображения в ряде электростатических задач облегает построение решения.
. Способ отыскания конформного
отображения в ряде электростатических задач облегает построение решения.
В качестве примера
нахождения комплексного потенциала рассмотрим задачу, решение которой известно.
Поле заряженной бесконечно тонкой прямой нити, совпадающей с осью ![]() , в цилиндрической системе координат имеет
вид
, в цилиндрической системе координат имеет
вид
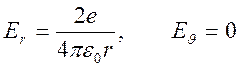 ,
,
где![]() - заряд
единицы длины нити. Найдем представление для комплексного потенциала
- заряд
единицы длины нити. Найдем представление для комплексного потенциала ![]() . Так как
. Так как
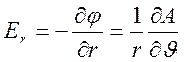 ,
,
то 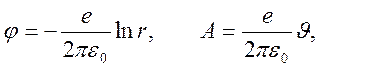 .
Комплексный потенциал имеет вид
.
Комплексный потенциал имеет вид
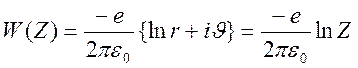 ,
, ![]() .
.
5.7.
Сведение объемных сил в электростатике к
поверхностным натяжениям. Тензор натяжения. Найдем выражение для силы действующей со стороны электростатического
поля на заряды в объеме ![]()
вещества. Пусть распределение зарядов в этом объеме характеризуется
плотностью ![]() . Сторонние заряды создают
электростатическое поле
. Сторонние заряды создают
электростатическое поле ![]() и статическое
распределение свободных зарядов. На заряды в элементе объема
и статическое
распределение свободных зарядов. На заряды в элементе объема ![]() действует сила
действует сила ![]() ,
которую с учетом уравнения
,
которую с учетом уравнения
![]()
можно записать в виде
![]() .
.
Тогда полная сила, действующая на заряды в объеме ![]() , запишется следующим образом
, запишется следующим образом
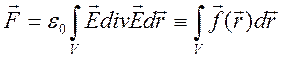 , (5.11)
, (5.11)
где
![]() - вектор плотности объемной силы.
Представим выражение для силы
- вектор плотности объемной силы.
Представим выражение для силы ![]() через поверхностный
интеграл. Такое представление имеет то преимущество, что вместо трехкратного
интеграла (5.11) можно получить двукратный интеграл, который требует знания
подынтегральной функции не в объеме
через поверхностный
интеграл. Такое представление имеет то преимущество, что вместо трехкратного
интеграла (5.11) можно получить двукратный интеграл, который требует знания
подынтегральной функции не в объеме ![]() , а только на окружающей
его поверхности
, а только на окружающей
его поверхности ![]() . С этой целью к выражению для
. С этой целью к выражению для ![]() добавим нулевое слагаемое
добавим нулевое слагаемое ![]() (в электростатике
(в электростатике ![]() ).
Тогда компоненты вектора
).
Тогда компоненты вектора ![]() можно будет записать
через дивергенцию некоторых векторов. Это даст возможность использовать формулу
Гаусса – Остроградского и перейти от объемного интеграла к интегралу по
поверхности. Запишем
можно будет записать
через дивергенцию некоторых векторов. Это даст возможность использовать формулу
Гаусса – Остроградского и перейти от объемного интеграла к интегралу по
поверхности. Запишем ![]()
![]() .
Получим представление
.
Получим представление
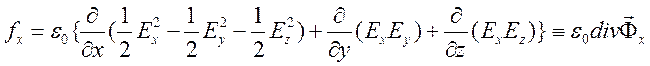 ,
,
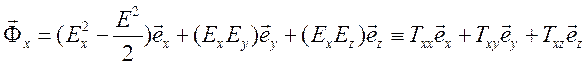 .
.
В
аналогичном виде можно представить и другие компоненты вектора ![]() . С помощью компонент
. С помощью компонент ![]() образуется тензор
образуется тензор ![]() .
.
Составляющие
вектора ![]() преобразуем, используя формулу Гаусса –
Остроградского
преобразуем, используя формулу Гаусса –
Остроградского
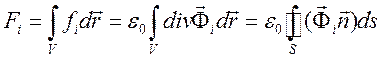 .
.
Эти
соотношения можно представить в компактной форме, введя тензор поверхностного
натяжения Максвелла ![]() :
:
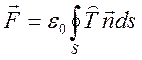 ,
, ![]() ,
,
Где
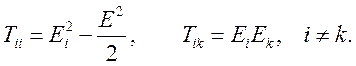
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.