Электростатика проводников. Основные закономерности электростатических полей, страница 4

       В разделе (3.3) было получено следующее выражение для плотности электрической энергии в среде с диэлектрической проницаемостью

                                                       ,

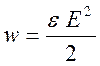значит, энергия плоского конденсатора, с учетом того, что между обкладками конденсатора , имеет представление

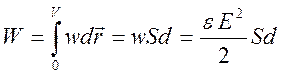                                           ,                   (5.5)

где  - площадь обкладки,  - расстояние между обкладками,  - объем между обкладками.. Напомним связь электрического поля с поверхностной плотностью зарядов на поверхности проводника :

                                           .

Так как 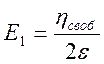 - напряженность поля, создаваемого одной пластиной конденсатора, то каждая из пластин испытывает со стороны другой пластины силу притяжения

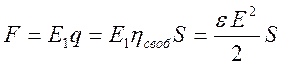                                           ,                               (5.5a)

где учтено, что .

Сравнение правых частей равенств (5.5) и (5.5а) показывает, что работа по раздвижению пластин на расстояние  совпадает с энергией (5.5)

                                           .

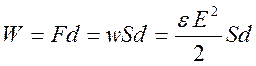         На заряженный проводник действуют силы со стороны им же создаваемого поля. Заряды находятся на поверхности проводника, и они отталкиваются друг от друга. Значит, эти силы приложены к поверхности, то есть носят характер сил натяжения или внутреннего давления. На единицу поверхности действует сила

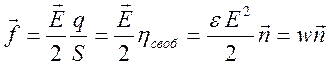                                                                   (5.6)

где  - единичная внешняя нормаль к поверхности проводника. На поверхности проводника действуют силы «отрицательного давления», направленного по внешней нормали.

Множитель  входит в (5.6) потому, что нужно учитывать только поле, которое создается всеми элементами поверхности за вычетом рассматриваемого элемента, а это поле равно половине полного поля.

       Под действием электрических сил происходит деформация проводника (изменение объема и формы), это явление называется электрострикцией. Ввиду растягивающего характера сил, объем проводника увеличивается. Если деформация слаба, то влияние изменения формы на изменение объема является эффектом второго порядка малости. В первом приближении изменение объема можно рассматривать как результат деформирования без изменения формы (всестороннее растяжение под действием некоторого избыточного давления равномерно распределенного по поверхности тела).

Энергия взаимодействия системы зарядов имеет вид

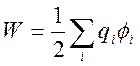                                                       ,                               (5.7)

где  - потенциал электрического поля, действующего на заряд. Покажем, что энергия (5.7) не имеет как функция координат минимума (это теорема Ирншоу).

       Условие наличия минимума  дается системой уравнений

                               ,

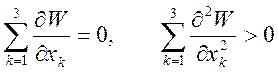однако, эти условия не выполняются, так как потенциалы  удовлетворяют уравнению Лапласса

                                           .

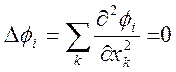Значит 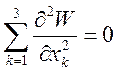. Таким образом, система заряженных части и тел не может находиться в равновесном состоянии под действием сил только электростатической природы. Для обеспечения равновесия необходимы силы иной (не электростатической) природы.

Приведем без доказательства два утверждения, характеризующие электростатическую энергию проводников

1.  Заряды, вносимые на проводники, располагаются на их поверхностях таким образом, чтобы энергия возникающего электростатического поля была минимальной (теорема Томсона).

2.  Внесение незаряженного проводника в поле фиксированной совокупности зарядов всегда приводит к уменьшению энергии поля.

5.5. Электрический диполь и квадруполь. К понятию электрического диполя можно придти различными способами.

Способ №1. Рассмотрим систему из двух разнесенных на фиксированное расстояние точечных электрических зарядов, равных по значению и противоположных по знаку. Такая система называется диполем, если если расстояние между зарядами мало по сравнению с расстоянием от них до точки наблюдения. Согласно принципу линейной суперпозиции, потенциал в точке  (Рис 5.2) можно представить в виде

                               ,

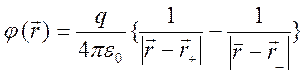где  - радиус векторы точек расположения наблюдателя и зарядов. Для упрощения расчетов начало координат расположено в средней точке между зарядами. Эта формула упрощается в наиболее интересном для приложений случае: , когда возможно использовать приближения