Электростатика проводников. Основные закономерности электростатических полей, страница 2

5. Из граничного условия

                                                        

с учетом того, что внутри проводника ,

получим соотношение на границе раздела

                                                                                          (5.1)

6. Соотношение (5.1) позволяет установить связь между полным зарядом  на поверхности проводника и потенциалом электрического поля. Если проводник окружен однородным диэлектриком, в котором нет пространственной дисперсии, то в рамках линейной электродинамики . Если  то условие (5.1) дает представление

                                           .

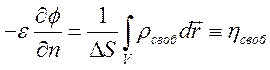Интегрируя это равенство по поверхности проводника , получим запись закона Кулона в терминах потенциала

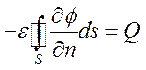                                                                   (5.2)

7. Так как электрическое поле и объемная плотность зарядов внутри проводника равны нулю, то при удалении из проводника части вещества, поле в возникшей полости по - прежнему остается равным нулю. Этот факт лежит в основе способа электростатической защиты. Для защиты объекта от действия электростатических полей следует окружит его металлической оболочкой. Если оболочку сделать в виде сетки, то «провисание» электрического поля внутрь оболочки будет происходить на расстояние сравнимое с размером отверстия.

8. Рассмотрим проводник, состоящий из двух металлических сфер радиусов  и , соединенных тонкой проволокой. Потенциалы этих сфер должны быть одинаковыми, так как они соединены проводником

                               .                      (5.2а)

В (5.2) равенства тем точнее, чем тоньше радиус проволоки. Так как

                                           ,

то следствием (5.2а) и граничного условия (5.1) является соотношение

                                           .

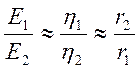Этот результат верен и в общем случае: чем меньше радиус кривизны проводника, тем больше напряженность поля вблизи его и тем больше поверхностная плотность заряда. Поэтому особенно велики эти значения вблизи острых краев проводников.

5.2. Электростатическая индукция. Выясним, что произойдет, если незаряженный проводник внести в электростатическое поле, созданное внешними (сторонними зарядами), положение которых зафиксировано. Электростатическое поле внутри проводника равно нулю. Но до внесения проводника, поле в объеме, который впоследствии занимает проводник, было отлично от нуля. В окончательном состоянии  это поле обращается в ноль. Следовательно, на проводнике, внесенном в электростатическое поле, должны возникнуть электрические заряды, поле которых, накладываясь на поле сторонних зарядов, должно приводить к полной компенсации поля внутри проводника. Это явление – возникновение зарядов на проводнике, внесенном в электростатическое поле, - называется электростатической индукцией. Из закона сохранения заряда следует, что суммарный заряд, индуцируемый на проводнике должен быть равен нулю. Вычисление плотности поверхностных зарядов на проводнике помещенном в электрическое поле, в общем случае представляет собой сложную задачу.

5.3. Электрическая емкость проводника.     Во многих задачах электростатики важную роль играет понятие емкости проводника и емкости системы проводников в диэлектрике. Если на уединенный проводник передать заряд, то он распределится по поверхности проводника так, что поверхность станет эквипотенциальной. Так как электрическое поле выражается через градиент потенциала, то потенциал можно задавать с точностью до постоянного слагаемого. Будем считать потенциал, создаваемый зарядом на проводнике, равным нулю на бесконечном расстоянии от проводника. Тогда, если увеличить в несколько раз заряд проводника, во столько же раз увеличится и потенциал проводника – это следствие линейной связи (рассматривается линейная электростатика)

                                                       ,       ,

где  - коэффициент пропорциональности, зависящий от формы и размера проводника. Его называют электрической емкостью, или просто емкостью. Единицу емкости в системе СИ называют фарад (); . С учетом (5.2) получаем представление

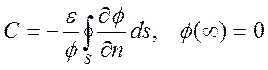                                                       . Для системы из  проводников линейная связь между  - зарядом  - го проводника и потенциалами всех проводников описывается с помощью коэффициентов взаимной емкости