Электростатика проводников. Основные закономерности электростатических полей, страница 5

                   .

Формула (5.7) упрощается, так как имеет место представление

.

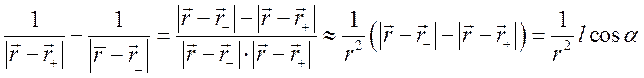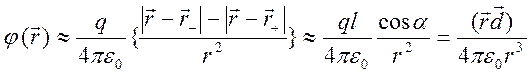       ,             (5.8)

где 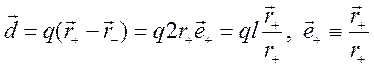 - электрический момент диполя. Электрическое поле имеет вид

,

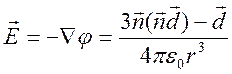где .

Абсолютная величина поля дается соотношением,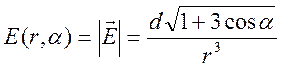

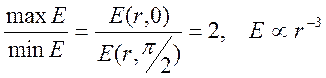. Напомним, что для точечного заряда имеет место более медленное убывание поля: .

       Если диполь помещен во внешне электрическое поле , то его потенциальная энергия это суперпозиция потенциальных энергий зарядов

                                      ,

где  - потенциал поля . Если  меняется мало на длине , то  и имеем

                                                    .

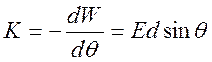Если диполь жесткий (), то момент силы , или .

Способ №2 введения понятия электрический диполь. Найдем потенциал системы зарядов вдали от этой системы.

                               ,

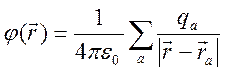где  - радиус – вектор заряда . Разложим это выражение в ряд по степеням :  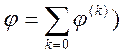                  , где .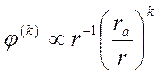

Функция , раскладывается в ряд по полиномам Лежандра ( - угол между векторами , см. Рис. 5.3). По сути, Здесь используется метод разделении переменных, который будет рассматриваться в разделе 5.6

      

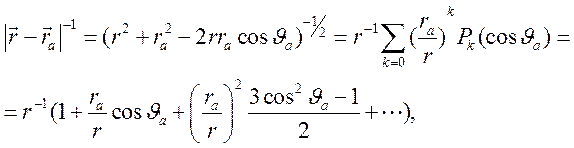
где

                                          

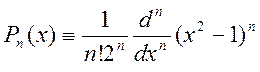
Тогда

                                          

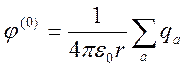
-  это потенциал, создаваемый суммарным зарядом системы, помещенный в начало координат (начало координат выбирается внутри системы). Если система в целом электронейтральна, то . Для  получается представление

-                                       ,                       .

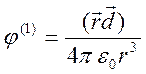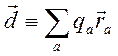дипольный момент  зависит от выбора начала координат. Смещение начала координат на вектор  изменяет дипольный момент на 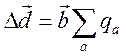. Эта зависимость пропадает только в электронейтральной среде. Получили обобщение понятия потенциала диполя и дипольного момента на случай системы многих зарядов. 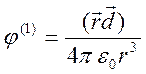 - это потенциал, помещенного в начало координат  фиктивного диполя с дипольным моментом . Имеет место разложение в ряд

                                           .

Левая часть этой формулы не зависит от выбора начала отсчета, а отдельные члены правой части – зависят. Для электронейтральной системы потенциал не зависит от выбора начала отсчета. Если система состоит из двух равных зарядов, противоположных по знаку, то  соответствует потенциалу диполя (5.8). Член  - представляет собой потенциал фиктивного квадруполя с соответствующим квадрупольным моментом. Выражение для него и для последующих членов мультипольного разложения потенциала здесь не приводим.

5.6. Методы решения электростатических задач. Задачи электростатики сводятся к решению уравнения Лапласа при заданных граничных условиях на некоторых поверхностях. Эти вопросы изучаются в курсе математической физики, здесь ограничимся указанием некоторых простых приемов и решением типичных задач.

       Метод изображений. Этот метод основан на том, что в электростатическом поле любую эквипотенциальную поверхность  можно заменить проводящей поверхностью с тем же потенциалом. При этом поле в пространстве не изменяется. Если интересоваться полем только с одной стороны такой проводящей поверхности, то всю часть пространства по другую сторону этой поверхности можно считать проводящей. Таким образом, задаче о поле зарядов при наличии проводящего тела можно сопоставить эквивалентную задачу о поле в пространстве без проводника, но с дополнительными зарядами (изображениями), которые создавали бы на поверхности, совпадающей с поверхностью проводника, тот же самый потенциал, каким обладал проводник. При рассмотрении задач электростатики диэлектриков (раздел 6.2) также используется метод изображений, но с несколько иной идеологией.

Простейший пример построения изображения точечного заряда в случае проводящей плоскости приведен на Рис. 5.4.

       Решим с помощью метода изображений более сложную задачу о поле точечного заряда  при наличии проводящего шара. Начало системы координат выберем в центре шара. Радиус его обозначим через  (Рис. 5.5). В точке  расположен точечный заряд . Необходимо найти потенциал . Возможна постановка двух задач (типа А и типа Б).

       Задача типа А). На поверхности шара задан потенциал , в частности . Последнее условие может создаваться за счет заземления.