Электростатика проводников. Основные закономерности электростатических полей, страница 7

Метод разделения переменных. Решение, зависящее от нескольких переменных, строится в виде суперпозиции вспомогательных функций, представляющих собой произведения функций. Каждая из последних функций зависит только от одной переменной. В уравнении для вспомогательных функций происходит разделение переменных. Такой прием использовался нами раньше (раздел 5.5) при нахождении поля системы точечных зарядов. Этот метод применяется также в задачах электростатики диэлектриков (раздел6.3) и в задачах электродинамики, когда поля зависят от времени.

            Применение метода рассмотрим на примере задачи о влиянии проводящей сферы (Рис. 5.7) на внешнее постоянное поле 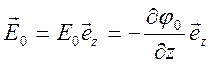, (). Решение задачи должно обладать свойством осевой симметрии, оно удовлетворяет уравнению Лапласа в сферической системе координат

                                    ,                                              (5.10)

где проводящая сфера является координатной поверхностью ,            ,        ,               .

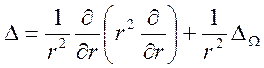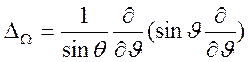Потенциал такой задачи  можно представить в виде суммы потенциала внешнего поля  и потенциала , описывающего влияние металлической сферы. Потенциал  удовлетворяет уравнению (5.10) и граничному условию, соответствующему заземлению сферы

                        .

Частное решение (из суперпозиции таких решений будет строиться ) уравнения (5.10) возьмем в виде произведения двух функций, зависящих от одной переменной

                                    .

В уравнении для  происходит разделение переменных и (5.10) представляется в виде

                                    .

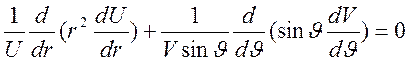Первое слагаемое в уравнении зависит только от , а второе слагаемое зависит только от . Это означает, что каждое из этих слагаемых есть величина постоянная, и сумма этих постоянных равна нулю

                                    .

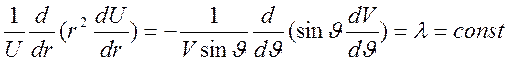Получили вместо уравнения в частных производных два обыкновенных дифференциальных уравнения для  и для .

Уравнение для функции  - это уравнение Лежандра

                                    .

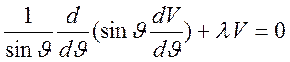Оно имеет два линейно независимых решения. Одно из решений является ограниченным при всех значениях аргумента , если выполняется условие

                                                ,

при этом функция Лежандра становится полиномом Лежандра

                                                .

Для этого полинома имеет место определение

                                                .

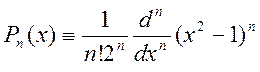Первые три члена этого ряда имеют вид

                       

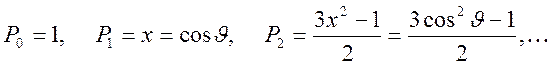
            Для частного решения  имеем уравнение

                        .

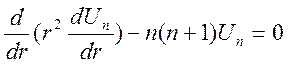Решение можно найти в виде , где ,  удовлетворяет уравнению,

                                                ,

имеющему два корня . Следовательно, получаем представление

                                    .

Так как на бесконечности должно выполняться условие , то необходимо взять . В результате получаем частное решение

                                    .

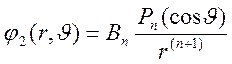Общее решение для потенциала , описывающего возмущение поля за счет проводящего шара, будем строить в виде суперпозиции частных решений

                                    .

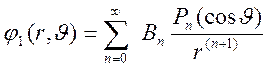Потенциал невозмущенного поля можно представить в виде

                                    ,

            Решение задачи  должно удовлетворять граничному условию на поверхности проводящего шара . Это условие дает уравнение для нахождения коэффициентов

                                    .

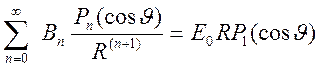Полиномы Лежандра взаимно ортогональны, поэтому получаем

                        при .

Значит,

                        .

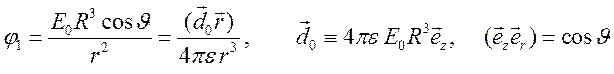            Таким образом, проводящая заземленная сфера (потенциал поверхности равен нулю), помещенная в однородное внешнее электрическое поле , приводит к возмущению поля в области  такому же, какое создает помещенный в центр сферы фиктивный точечный диполь с дипольным моментом .

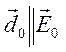            Использованный прием разложения решения по полиномам Лежандра часто применяется в задачах, решаемых в сферической системе координат. Удобство такого разложения обусловлено ортогональностью и полнотой системы полиномов Лежандра.

Метод конформного отображения. Если электростатическое поле зависит только от двух декартовых координат , то возможно использование аппарата теории функций комплексного переменного.