![]() .
.
Если приблизить к заряженному проводнику другие незаряженные проводники, то его потенциал уменьшится, так как на соседних проводниках индуцируются заряды при этом ближе к заряженному проводнику индуцируются заряды противоположного знака. Это уменьшение потенциала заряженного проводника при приближении к нему незаряженных проводников можно интерпретировать, как увеличение емкости заряженного проводника. Особенно сильно увеличится емкость проводника, если его окружить заземленным проводником. В этом случае индуцированные на замкнутом проводнике заряды того же знака, что и заряд внутреннего проводника, уйдут в землю. Общий индуцированный заряд противоположного знака по модулю равен заряду внутреннего проводника., так как все силовые линии, исходящие из внутреннего проводника, заканчиваются на окружающем его проводнике.
В случае
двух проводников с зарядами ![]() и
и ![]() , заряд
, заряд![]() пропорционален
разности потенциалов этих проводников. Отношение заряда к разности потенциалов
называют емкостью системы, а саму систему – электрическим
конденсатором. Емкость конденсатора
пропорционален
разности потенциалов этих проводников. Отношение заряда к разности потенциалов
называют емкостью системы, а саму систему – электрическим
конденсатором. Емкость конденсатора
![]()
определяется только
геометрией проводников (обкладок конденсатора) и не зависит от заряда ![]() .
.
В качестве
примера определим емкость элемента длины бесконечного коаксиального кабеля
(Рис.5.1). Обозначим ![]() - радиусы внутреннего и внешнего
проводников, между которыми находится однородный диэлектрик без
пространственной дисперсии. Считаем, что заряды проводников на отрезке длины
кабеля
- радиусы внутреннего и внешнего
проводников, между которыми находится однородный диэлектрик без
пространственной дисперсии. Считаем, что заряды проводников на отрезке длины
кабеля ![]() имеют значения
имеют значения ![]() и (
и (![]() ). По определению емкости имеем
). По определению емкости имеем
![]() .
.
Для нахождения потенциала воспользуемся формулой
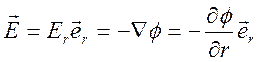 .
.
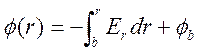
и получим
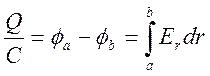 . (5.3)
. (5.3)
Найдем зависимость![]() от радиуса
от радиуса ![]() ,
воспользовавшись первичной (интегральной) формой уравнения
,
воспользовавшись первичной (интегральной) формой уравнения
![]()
![]() .
.
Соответствующая форма имеет вид
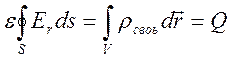 . (5.4)
. (5.4)
В качестве объема ![]() возьмем концентрический с коаксиальным
кабелем цилиндр радиуса
возьмем концентрический с коаксиальным
кабелем цилиндр радиуса ![]() (
(![]() ) и длины
) и длины ![]() .
Формула (5.4) принимает вид
.
Формула (5.4) принимает вид
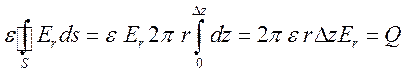 ,
,
![]() .
.
Подставляя это выражение в (5.3) получаем представление для емкости отрезка коаксиального кабеля
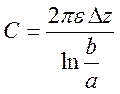 .
.
Величина емкости увеличивается при уменьшении расстояния между обкладкам конденсатора
5.4. Электростатическая энергия проводников. Теорема Ирншоу. При переносе на проводник новых зарядов, на них действует сила отталкивания со стороны уже находящихся на проводнике зарядов. Для преодоления этой силы необходимо совершить работу. В процессе зарядки проводника, одновременно происходит передача ему энергии.
Пусть на
проводник переносится заряд ![]() и пусть это происходит
в электростатическом поле этого заряда
и пусть это происходит
в электростатическом поле этого заряда ![]()
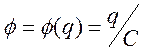 в отсутствии внешнего поля. При этом
совершается работа
в отсутствии внешнего поля. При этом
совершается работа 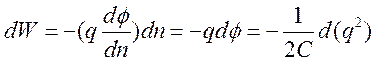 ,
,
где ![]() - емкость проводника. Значит, полная работа
при дополнительной зарядке проводника на величину
- емкость проводника. Значит, полная работа
при дополнительной зарядке проводника на величину ![]() в
линейной электростатике имеет вид
в
линейной электростатике имеет вид
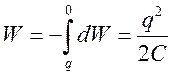 .
.
Эта работа
переходит в электростатическую энергию проводника. Если учесть
соотношение ![]() , где
, где ![]() -
потенциал проводника, имеющего заряд
-
потенциал проводника, имеющего заряд ![]() ,
, ![]() , то можно получить дополнительные
выражения для энергии проводника
, то можно получить дополнительные
выражения для энергии проводника
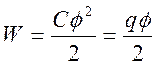 .
.
Следует отметить
наличие множителя ![]() в последней формуле, Это
произошло из за того, что потенциал
в последней формуле, Это
произошло из за того, что потенциал ![]() создавался самим
зарядом
создавался самим
зарядом ![]() . Если бы потенциал
. Если бы потенциал ![]() создавался
посторонними зарядами (сторонним полем), то энергия заряда
создавался
посторонними зарядами (сторонним полем), то энергия заряда ![]() в таком поле составила бы величину
в таком поле составила бы величину ![]() . В самом деле, совершается в такой
ситуации работа на участке
. В самом деле, совершается в такой
ситуации работа на участке ![]() имеет вид
имеет вид
 ,
,
где ![]() не зависит от
не зависит от ![]() .Полная
работа
.Полная
работа ![]() .
.
Если имеется
несколько проводников с зарядами ![]() и
и ![]() - потенциалы этих проводников, создаваемые
всеми зарядами, то их электростатическая энергия представляется в виде
- потенциалы этих проводников, создаваемые
всеми зарядами, то их электростатическая энергия представляется в виде
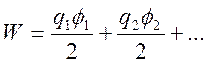 ,
,
в частности для конденсатора имеем
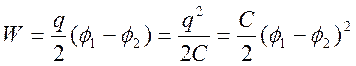 ,
,
где ![]() - заряд одной обкладки,
- заряд одной обкладки, ![]() - потенциалы обкладок,
- потенциалы обкладок, ![]() - емкость конденсатора.
- емкость конденсатора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.