4. Граничные условия.Уравнения Максвелла в интегральной форме. Граничные условия.
4.1. Уравнения Максвелла для материальных сплошных сред в интегральной форме. Граничные условия. Дифференциальные системы уравнений Максвелла для материальных сплошных средв четырех, приведенных выше формах, эквивалентны. Применимы они лишь для описания полей в областях, где нет разрывов (скачков) соответствующих функций. На поверхностях разрыва функций происходит обращение в бесконечность производных. Необходимо иметь граничные условия (соотношения на разрыве) для «сшивания» полей по разные стороны от поверхности разрыва. Такая ситуация возникает, в частности на фронтах ударных волн по причине проявления нелинейности. В линейных задачах разрывы полей возникают на поверхностях (контактные поверхности), разделяющих среды с различными свойствами. Конечно, такая трудность возникает из-за чрезмерной идеализации в постановке задачи. В линейной ситуации поля будут изменяться непрерывно, если заменить границу раздела сред неоднородной переходной областью. Однако это приводит к большому усложнению решения задачи. По этой причине часто используется более «грубая» идеализация резкой границы раздела сред. Боле первичными по отношению к дифференциальным уравнениям Максвелла являются уравнения Максвелла в интегральной форме. Переход от дифференциальных уравнений к уравнениям в интегральной форме неоднозначен. «Наиболее первичными», являются уравнения Максвелла в интегральной форме в виде законов сохранения. По сути, это первичные постулаты электродинамики сплошных сред (в рамках теории сплошной среды они ни откуда не выводятся). Из этих уравнений и получаются граничные условия. Отметим, что предельный переход от неоднородной переходной области к резкой границе раздела сред, дает те же граничные условия, что и уравнения в интегральной форме в виде законов сохранения. Это является дополнительным аргументом правильности граничных условий, получаемых из уравнений в интегральной форме.
Начнем
с вывода граничного условия для вектора магнитной индукции ![]() . Для этого используем интегральную форму
. Для этого используем интегральную форму
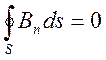 . (4.1)
. (4.1)
Связь уравнения (4.1) с известным нам дифференциальным уравнением
![]() (4.2)
(4.2)
можно
увидеть, если проинтегрировать (4.2) по объему и использовать формулу
Гаусса-Остроградского для перехода к виду (4.1). Применим (4.1) к цилиндру
высотой ![]() (Рис. 4.1) и осью, перпендикулярной к
границе раздела двух сред (1) и (2) и «вырезающему» из границы элемент поверхности
(Рис. 4.1) и осью, перпендикулярной к
границе раздела двух сред (1) и (2) и «вырезающему» из границы элемент поверхности
![]() Поток индукции в (4.1 ) складывается из
потока через боковую поверхность (при
Поток индукции в (4.1 ) складывается из
потока через боковую поверхность (при ![]() этот
поток стремится к нулю) и потока индукции через верхнее и нижнее основания
цилиндра. Выберем площадь оснований
этот
поток стремится к нулю) и потока индукции через верхнее и нижнее основания
цилиндра. Выберем площадь оснований ![]() настолько малой, чтобы
компоненты
настолько малой, чтобы
компоненты ![]() и
и ![]() в
пределах этих оснований в средах (1) и (2) были бы постоянными. Направления
нормалей
в
пределах этих оснований в средах (1) и (2) были бы постоянными. Направления
нормалей ![]() на основаниях цилиндра имеют
противоположные направления, поэтому имеем
на основаниях цилиндра имеют
противоположные направления, поэтому имеем ![]() ,
, ![]() и формула (4.1) принимает вид
и формула (4.1) принимает вид
![]() ,
,
или ![]() .
.
Это условие непрерывности нормальной к границе раздела сред компоненте вектора магнитной индукции.
Получим теперь граничное условие для вектора электрической индукции
![]() ,
,
входящий в третью форму уравнений Максвелла . От дифференциального уравнения
![]() (4.3)
(4.3)
можно
прейти к первичной интегральной форме следующим способом: проинтегрируем (4.3)
по объему ![]()
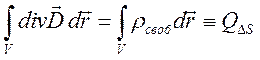 .
.
С учетом формулы Гаусса-Остроградского будем иметь первичную интегральную форму
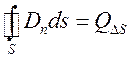 , (4.4)
, (4.4)
где
![]() - полный свободный заряд внутри объема
- полный свободный заряд внутри объема ![]() , ограниченного площадками
, ограниченного площадками ![]() .
.
Не следует воспринимать приведенные рассуждения, как вывод уравнения (4.4) из (4.3). На самом деле первичным является уравнение (4.4). Более того: уравнение (4.4) это постулат.
Используем в качестве ![]() поверхность
цилиндра, изображенного на Рис.4.1. Действуя аналогично тому, как это делалось
при выводе граничного условия для вектора
поверхность
цилиндра, изображенного на Рис.4.1. Действуя аналогично тому, как это делалось
при выводе граничного условия для вектора ![]() , получим
соотношение
, получим
соотношение
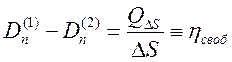 ,
,
где
![]() - плотность свободного поверхностного
заряда на границе раздела.
- плотность свободного поверхностного
заряда на границе раздела.
При
получении граничных условий для векторов ![]() и
и ![]() будем исходить из
будем исходить из
уравнений
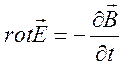 , (4.5)
, (4.5)
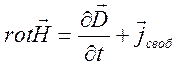 (4.6)
(4.6)
в
соответствующей им первичной интегральной форме. С этой целью выберем
прямоугольную площадку ![]() , перпендикулярную границе
раздела и ограниченную контуром
, перпендикулярную границе
раздела и ограниченную контуром ![]() (Рис.4.2). Направления
(Рис.4.2). Направления ![]() ортогональны друг другу.
ортогональны друг другу. ![]() - нормаль к границе раздела. Вектор
- нормаль к границе раздела. Вектор![]() - лежит в плоскости границы раздела и
вектор
- лежит в плоскости границы раздела и
вектор ![]() ортогонален площадке
ортогонален площадке ![]() . Интегрирование по площади
. Интегрирование по площади ![]() компонент уравнений (4.5), (4.6) по
направлению
компонент уравнений (4.5), (4.6) по
направлению ![]() и использование формулы Стокса, позволяет
перейти к первичной интегральной форме уравнений (4.5), (4.6)
и использование формулы Стокса, позволяет
перейти к первичной интегральной форме уравнений (4.5), (4.6)
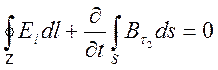 , (4.7)
, (4.7)
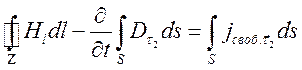 . (4.8)
. (4.8)
Выбирая
величину ![]() достаточно малой, и устремляя вертикальный
размер
достаточно малой, и устремляя вертикальный
размер ![]() к нулю (при этом площадь
к нулю (при этом площадь ![]() стремится к нулю), будем иметь
представления
стремится к нулю), будем иметь
представления
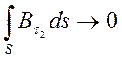 ,
, 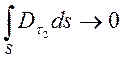 ,
,
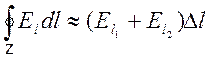 ,
, 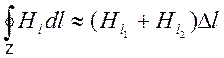 ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
получим из (4.7), (4.8) два граничные условия
![]() , (4.9)
, (4.9)
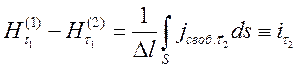 . (4.10)
. (4.10)
Здесь
![]() -плотность поверхностного тока проводимости
в направлении
-плотность поверхностного тока проводимости
в направлении ![]() . Так как выбор
. Так как выбор ![]() (и соответственно выбор направления
вектора
(и соответственно выбор направления
вектора ![]() ) произволен, граничное условие (4.9) можно
записать в виде
) произволен, граничное условие (4.9) можно
записать в виде
![]() ,
,
где![]() - произвольное касательное к границе
раздела сред направление. Аналогичные рассуждения, позволяют представить
граничное условие (4.10) в векторной форме
- произвольное касательное к границе
раздела сред направление. Аналогичные рассуждения, позволяют представить
граничное условие (4.10) в векторной форме
![]() ,
,
где
![]() - вектор плотности поверхностного тока
проводимости.
- вектор плотности поверхностного тока
проводимости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.