8. Магнитостатика.
Векторный потенциал в магнитостатике. Потенциал магнитного диполя.Потенциал магнитного диполя. Закон Био – Савара – Лапласса.Энергия магнитного поля системы линейных замкнутых контуров с током. Индуктивность. Индуктивность коаксиального кабеля. Магнитостатика в материальных средах.
8.1. Векторный потенциал в магнитостатике. Потенциал магнитного диполя. Закон Био – Савара – Лапласса. В магнитостатике имеют место уравнения
![]() , (8.1)
, (8.1)
![]() (8.2)
(8.2)
Из (8.1) следует возможность
введения векторного потенциала ![]()
![]() .
.
В случае ![]() и
и ![]() из
уравнения (8.2) получается уравнение для векторного потенциала
из
уравнения (8.2) получается уравнение для векторного потенциала
![]() .
.
Если вместо вектора ![]() выбрать вектор
выбрать вектор ![]() , то
будем иметь
, то
будем иметь ![]() . Это свойство векторного потенциала
называется градиентной инвариантностью. Используя эту инвариантность уравнение
для векторного потенциала можно упростить
. Это свойство векторного потенциала
называется градиентной инвариантностью. Используя эту инвариантность уравнение
для векторного потенциала можно упростить
![]() .
.
Выберем функцию ![]() так, чтобы
так, чтобы ![]() , тогда
будем иметь (ниже штрих для простоты написания опустим)
, тогда
будем иметь (ниже штрих для простоты написания опустим)
![]() , (8.3)
, (8.3)
![]() . (8.4)
. (8.4)
Уравнение (8.3) это векторное уравнение Пуассона.
В электростатике
уравнению Пуассона ![]() удовлетворяло решение в виде
суперпозиции (интеграла) вкладов от бесконечного числа точечных источников, если
отсутствовали поверхностные заряды
удовлетворяло решение в виде
суперпозиции (интеграла) вкладов от бесконечного числа точечных источников, если
отсутствовали поверхностные заряды
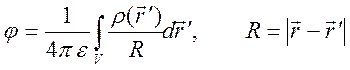 .
.
Аналогично можно записать
решение для ![]() :
:
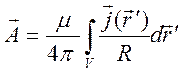 . (8.5)
. (8.5)
Из формулы (8.5) можно
получить закон Био – Савара – Лапласа. Покажем это на примере замкнутого тока,
протекающего по тонкому проводнику (Рис. 8.1). Будем считать, что расстояние ![]() от точки наблюдения до точек источника
удовлетворяет условиям
от точки наблюдения до точек источника
удовлетворяет условиям
![]() ,
,
где ![]() -
длина проводника,
-
длина проводника, ![]() - его поперечное сечение. Полный
ток в проводнике не зависит от времени (рассматривается статическая ситуация) и
не зависит от координат
- его поперечное сечение. Полный
ток в проводнике не зависит от времени (рассматривается статическая ситуация) и
не зависит от координат
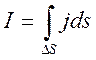 .
.
Преобразуем (8.5)
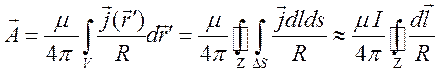 .
.
Здесь учтено, что на
поверхности сечения ![]() в силу условия
в силу условия ![]() , расстояние
, расстояние ![]() и
направление векторов
и
направление векторов ![]() можно считать постоянными и
вынести за знак интеграла по
можно считать постоянными и
вынести за знак интеграла по ![]() . Таким образом,
получаем формулу для потенциала замкнутого линейного тока
. Таким образом,
получаем формулу для потенциала замкнутого линейного тока
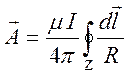 . (8.6)
. (8.6)
Получим формулу
для поля ![]() , создаваемого линейным замкнутым током на
основе представления (8.6) для векторного потенциала. Меняя местами операции
дифференцирования и интегрирования (дифференцирование производится по
координатам точки наблюдения, а интегрирование ведется по координатам
источника):
, создаваемого линейным замкнутым током на
основе представления (8.6) для векторного потенциала. Меняя местами операции
дифференцирования и интегрирования (дифференцирование производится по
координатам точки наблюдения, а интегрирование ведется по координатам
источника):
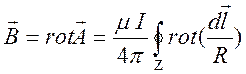 .
.
Используем формулу ![]() , где
, где ![]() , так
как
, так
как ![]() не зависит от координат точки наблюдения.
Имеем
не зависит от координат точки наблюдения.
Имеем
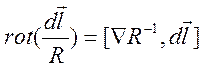 ,
,
где 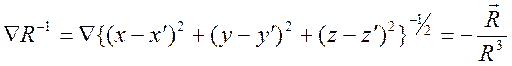 .
Приходим к закону Био - Савара - Лапласса
.
Приходим к закону Био - Савара - Лапласса
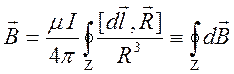 ,
,
где введено обозначение 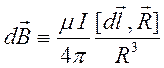 - поле, создаваемое в точке наблюдения
элементом тока длиной
- поле, создаваемое в точке наблюдения
элементом тока длиной ![]() . Напомним, что понятие линейного
тока пригодно только на больших расстояниях от источника при условии
. Напомним, что понятие линейного
тока пригодно только на больших расстояниях от источника при условии ![]() и это понятие теряет смысл вблизи
проводника.
и это понятие теряет смысл вблизи
проводника.
Введем среднее расстояние ![]() от точки наблюдения до контура с током.
Так как
от точки наблюдения до контура с током.
Так как ![]() , то в формуле (8.6) можно использовать
разложение
, то в формуле (8.6) можно использовать
разложение
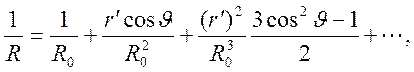 (8.7)
(8.7)
где ![]() -
радиус вектор точки интегрирования на контуре с током,
-
радиус вектор точки интегрирования на контуре с током, ![]() -
угол между векторами
-
угол между векторами ![]() и
и ![]() .
Подставляя (8.7) в (8.6), получим
.
Подставляя (8.7) в (8.6), получим
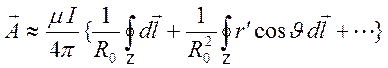 . (8.8)
. (8.8)
Первое слагаемое в (8.8) для
замкнутого контура равно нулю, второе слагаемое является главным и представляет
собой потенциал магнитного диполя. На больших расстояниях имеем
закономерность ![]() . В силу формулы
. В силу формулы ![]() получаем закон убывания с расстоянием
магнитной индукции
получаем закон убывания с расстоянием
магнитной индукции ![]() . Напомним, что электрическое
поле замкнутой электронейтральной системы зарядов на больших расстояниях
изменяется по закону
. Напомним, что электрическое
поле замкнутой электронейтральной системы зарядов на больших расстояниях
изменяется по закону ![]() .
.
8.2. . Энергия магнитного поля системы линейных замкнутых контуров с током. Индуктивность. Индуктивность коаксиального кабеля. Для энергии магнитного поля имеется представление
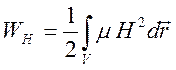 . (8.9)
. (8.9)
Ниже ограничимся
рассмотрением случая ![]() и учтем соотношения
и учтем соотношения
![]() .
.
Формулу (8.9) представим в виде
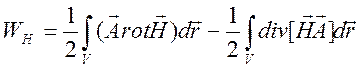 ,
,
где согласно формуле Гаусса – Остроградского имеем
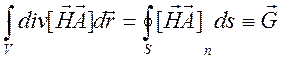 .
.
В качестве объема ![]() возьмем все пространство, тогда
возьмем все пространство, тогда ![]() и для магнитной энергии имеем
представление
и для магнитной энергии имеем
представление
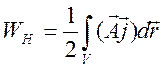 . (8.10)
. (8.10)
Интегрирование здесь
производится только по объему источника, где ![]() . На
основе (8.10) получим выражение для магнитной энергии системы из
. На
основе (8.10) получим выражение для магнитной энергии системы из ![]() линейных контуров с током.
линейных контуров с током.
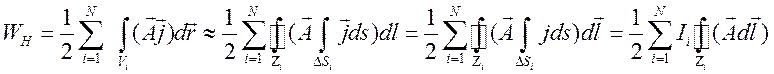 .
.
Вектор ![]() вынесен из под знака интеграла по
вынесен из под знака интеграла по ![]() , так как для линейных токов
, так как для линейных токов ![]() приближенно постоянен на поперечном
сечении
приближенно постоянен на поперечном
сечении ![]() . Приходим к формуле
. Приходим к формуле
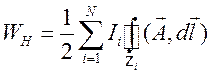 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.